Hostname: page-component-6dbcb7884d-4vmf6 Total loading time: 0 Render date: 2025-02-14T08:53:06.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant theory and Steenrod operations – maps between rings of invariants

Published online by Cambridge University Press:  24 October 2008

Zafer Mahmud  and
Larry Smith
Zafer Mahmud
Affiliation:
Department of Mathematics, University of Kuwait, Kuwait City, Kuwait e-mail: [email protected]
Larry Smith
Affiliation:
Mathematisches Institut der Universität, Bunsenstrasse 3–5, D 37073 Göttingen, Germany e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G ′, G ″ be finite groups and p ′: G ↪ GL(n ′,ℚ), p ″: G ″ ↪ GL(n ″, ℚ) faithful rational representations. If T: V′ = ℚn′ → ℚn″ = V ″ is a linear transformation and Ξ: G ′ → G ″ a function such that

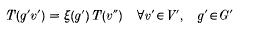
then there are induced algebra homomorphisms ℚ[V ″] → ℚ[V ] and ℚ[V ″]G ″ → ℚ[V ′]G ′ making the diagram

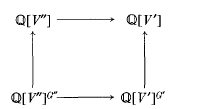
commute. In this note we isolate the invariant theory portion of [1] and extend it to provide a necessary and sufficient condition that an algebra homomorphism between rings of invariants ℚ[V ″]G ″ → ℚ[V ′]G ′ arises in this way.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 1 , July 1996 , pp. 103 - 116
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, J. F. and Mahmud, Z.. Maps between classifying spaces. Inventiones Math. 35 (1976), 1–41.CrossRefGoogle Scholar
[2]Lang, S.. Algebraic number theory (Springer-Verlag, 1994).CrossRefGoogle Scholar
[3]Smith, L.. Realizing nonmodular polynomial algebras as the cohomology of spaces of finite type fibered over × BU(d). Pacific J. of Math. 127 (1987), 361–387.CrossRefGoogle Scholar
[4]Smith, L.. Polynomial invariants of finite groups (A. K. Peters Ltd, 1995).CrossRefGoogle Scholar
[5]Smith, L.. -Invariant ideals in rings of invariants. Forum Math., to appear.Google Scholar
[6]Smith, L. and Stong, R. E.. On the invariant theory of finite groups: orbit polynomials and splitting principles. J. Algebra 110 (1987), 134–157.Google Scholar
[7]Weyl, H.. The classical groups, second edition (Princeton University Press, 1946).Google Scholar