Integrals and derivatives of functions in MacLane's class 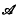 and of normal functions†
and of normal functions†
Published online by Cambridge University Press: 24 October 2008
Extract
If f is meromorphic in D = {,|z| < 1}, we say that f has the asymptotic value a at ζ, ζ ∈ C(={|z| = 1}), if there exists an arc Γ such that Γ ends at ζ, (Γ − {ζ}) ⊂ D, and f has the limit a as |z| → 1 on Γ. The class 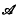 (
(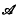 M) originally defined by G. R. MacLane ((8), p. 8), consists of those functions that are non-constant and holomorphic (meromorphic) in D and that have asymptotic values at a dense subset of C. In (8), p. 36, MacLane has shown the following three conditions are sufficient for a non-constant holomorphic function f to be in
M) originally defined by G. R. MacLane ((8), p. 8), consists of those functions that are non-constant and holomorphic (meromorphic) in D and that have asymptotic values at a dense subset of C. In (8), p. 36, MacLane has shown the following three conditions are sufficient for a non-constant holomorphic function f to be in 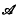 :
:
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 1 , January 1972 , pp. 111 - 121
- Copyright
- Copyright © Cambridge Philosophical Society 1972
References
REFERENCES
- 1
- Cited by


