Published online by Cambridge University Press: 24 October 2008
Let Ωn denote the convex set of all n × n doubly stochastic matrices: chat is, the set of all n × n matrices with non-negative entries and row and column sums 1. If A = (aij) is an arbitrary n × n matrix, then the permanent of A is the scalar valued function of A defined by
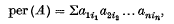
where the subscripts i1, i2, …, in run over all permutations of 1, 2, …, n. The permanent function has been studied extensively of late (see, for example, (1), (2), (3), (4), (6)) and it is known that if A ∈ Ωn then 0 < cn ≤ per (A) ≤ 1, where the constant cn depends only on n. It is natural to inquire if per (A) is a convex function of A for A ∈ Ωn. That this is not the case was shown by a counter-example given by Marcus and quoted by Perfect in her paper ((5)). In this paper, however, she shows that per (½I + ½A) ≤ ½ + ½ per (A) for all A ∈ Ωn. Here I = In is the identity matrix of order n.