No CrossRef data available.
Published online by Cambridge University Press: 27 November 2024
Let  $r_5(N)$ be the largest cardinality of a set in
$r_5(N)$ be the largest cardinality of a set in  $\{1,\ldots,N\}$ which does not contain 5 elements in arithmetic progression. Then there exists a constant
$\{1,\ldots,N\}$ which does not contain 5 elements in arithmetic progression. Then there exists a constant 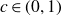 $c\in (0,1)$ such that
$c\in (0,1)$ such that  \[r_5(N)\ll \frac{N}{\exp\!((\!\log\log N)^{c})}.\]
\[r_5(N)\ll \frac{N}{\exp\!((\!\log\log N)^{c})}.\] $U^4$-inverse theorem of J. Leng and the fact that 3-step nilsequences may be approximated by locally cubic functions on shifted Bohr sets. This, combined with the density increment strategy of Heath–Brown and Szemerédi, codified by Green and Tao, gives the desired result.
$U^4$-inverse theorem of J. Leng and the fact that 3-step nilsequences may be approximated by locally cubic functions on shifted Bohr sets. This, combined with the density increment strategy of Heath–Brown and Szemerédi, codified by Green and Tao, gives the desired result.
Leng supported by an NSF Graduate research fellowship grant no. DGE-2034835.
Sah and Sawhney were supported by NSF Graduate research fellowship program DGE-2141064.