Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eckmann, B.
and
Hilton, P. J.
1960.
Homotopy groups of maps and exact sequences.
Commentarii Mathematici Helvetici,
Vol. 34,
Issue. 1,
p.
271.
Hilton, P. J.
and
Ledermann, W.
1960.
Homology and Ringoids. III.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 56,
Issue. 1,
p.
1.
Puppe, Dieter
1962.
Korrespondenzen in abelschen Kategorien.
Mathematische Annalen,
Vol. 148,
Issue. 1,
p.
1.
Sehgal, S. K.
1964.
Ringoids with minimum condition.
Mathematische Zeitschrift,
Vol. 83,
Issue. 5,
p.
395.
Gaines, Fergus J.
and
Laffey, Thomas J.
1985.
The mathematical work of Walter Ledermann.
Linear Algebra and its Applications,
Vol. 69,
Issue. ,
p.
1.
Hazewinkel, M.
1992.
Encyclopaedia of Mathematics.
p.
1.
Skornyakov, L. A.
Mysovskikh, I. P.
Talalyan, A. A.
Solomentsev, E. D.
Sveshnikov, A. G.
Chuyanov, V. A.
Shmel’kin, A. L.
Andrunakievich, V. A.
Minlos, R. A.
Bulota, K. Yu.
Kuz’min, L. V.
Mineev, M. P.
Sevast’yanov, B. A.
Cnentsov, N. N.
Dobrushin, R. L.
Prelov, V. V.
Prokhorov, Yu. V.
Yaglom, A. M.
Kolchin, V. F.
Pagurova, V. I.
Borovkov, A. A.
Nikulin, M. S.
Popova, T. Yu.
Ivanova, O. A.
Popov, V. L.
Govorov, V. E.
Fedoryuk, M. V.
D’yakonov, E. G.
Dolzhenko, K. P.
Kulikov, Viktor S.
Sullivan, D.
Kudryavtsev, L. D.
Kulikov, Val. S.
Rapinchuk, A. S.
Malyshev, A. V.
Dellacherie, C.
Babich, V. M.
Prokhorov, A. V.
Rozov, N. Kh.
Fife, P. C.
Gudkov, D. A.
Ponomarev, D. A.
Plisko, V. E.
Stepanov, S. A.
Golubov, B. I.
Artemov, S. N.
Millionshchikov, K. M.
Millionshchikov, V. M.
Belyakin, N. V.
Dushskiĭ, V. A.
Rousseeuw, P. J.
Domanskiĭ, V. K.
Goncharov, S. S.
Degtev, A. N.
Tankeev, S. G.
Grishin, V. N.
Millwnshchikov, V. M.
Alekseevskiĭ, D. V.
Shevrin, L. N.
Turchin, V. F.
Arkhangelskiĭ, A. V.
Vinberg, E. B.
Dolzhenko, E. P.
Vil’yams, N. N.
Solomentsev, E. V.
Buevich, V. A.
Vapnyarskiĭ, I. B.
Vladimirov, U. A.
Viil’yams, N. N.
Ivanov, A. B.
Danilov, V. I.
Shevnn, L. N.
Terekhin, A. P.
Ilyashenko, Yu. S.
Skiĭ, A. V. Arkhangel
Volkov, J. J.
Platonov, V. P.
Volkov, I. I.
Arsenin, V. Ya.
Tikhonov, A. N.
Mishchenko, A. S.
Norden, A. P.
Mikhalev, A. V.
Sklyarenko, E. G.
Sokolov, D. D.
Ruzmaĭkin, A. A.
Nikolaev, E. S.
Karpova, N. A.
Yablonskiĭ, S. V.
Belyaev, Yu. K.
Gnedenko, B. V.
Sevast’yanov, V. A.
Anikin, S. A.
Tsalenko, M. Sh.
Onishchik, A. L.
Rudakov, A. N.
Ringel, C. M.
Gluskin, L. M.
Lyapin, E. S.
Shtern, A. I.
Roĭter, A. V.
Nagornyĭ, N. M.
Merzlyakov, Yu. I.
Golubov, E. A.
Yuzhakov, A. P.
Sobolev, V. I.
Kuzmm, L. V.
Voĭtseknovskiĭ, M. I.
Butenin, N. V.
Bryuno, A. D.
Proskuryakov, I. V.
Nakhushev, A. M.
Arkhangel’skiĭ, A. V.
Malakhovskiĭ, V. S.
Tonkov, E. L.
Sidorov, L. A.
Sabitov, I. Kh.
Shardurov, V. V.
Konyushkov, A. A.
Gakhov, F. D.
Il’in, V. A.
Nakhyshev, A. M.
Chirka, E. M.
Lykashenko, T. P.
Krushkal’, S. L.
Lumiste, Ü.
Toponogov, V. A.
Burago, Yu. D.
Aleksandrov, A. D.
Berestovskiĭ, V. N.
Tikhomirov, V. M.
Lukashenko, T. P.
Emel’yanov, V. F.
Rudyak, Yu. B.
Kopytov, V. M.
Parshin, A. N.
Bakhturin, Yu. A.
and
Zhevlakov, K. A.
1995.
Encyclopaedia of Mathematics.
p.
715.
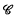 (with identities) as a set of elements α, β,… in which addition and multiplication are defined for certain pairs of elements in such a way that, whenever operations are defined, the usual ring axioms are satisfied. Precisely,
(with identities) as a set of elements α, β,… in which addition and multiplication are defined for certain pairs of elements in such a way that, whenever operations are defined, the usual ring axioms are satisfied. Precisely, 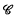 is an abstract category ((3), p. 108) with an addition operation such that the following axioms hold:
is an abstract category ((3), p. 108) with an addition operation such that the following axioms hold: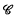 , let ℋ(ι, ι′) be the set of elements of
, let ℋ(ι, ι′) be the set of elements of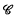 whose left identity is ι and right identity is ι′; then ℋ(ι, ι′) is empty or an Abelian group under addition.
whose left identity is ι and right identity is ι′; then ℋ(ι, ι′) is empty or an Abelian group under addition.