Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T13:41:11.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups with every proper quotient finite

Published online by Cambridge University Press:  24 October 2008

J. S. Wilson
J. S. Wilson
Affiliation:
Christ's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1·1. We shall write 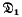for the class of groups all of whose non-trivial normal subgroups have finite index. Thus, rather obviously, finite groups, simple groups, and the infinite cyclic and dihedral groups all lie in the class 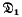. Other examples of 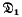-groups are to be found in a variety of contexts. The main result of Mennicke (8) shows that, for n ≥ 3, the factor group of SL(n, Z) by its centre is a 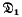-group, where SL(n, Z) denotes the unimodular group of all n × n invertible matrices with integer coefficients and with determinant 1. In McLain(7), an example is given of an infinite, locally finite, locally soluble 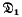-group, whose only non-trivial normal subgroups are the terms of its derived series, and in (4), P. Hall discusses an infinite 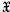-group, all of whose proper quotients are finite p-groups. If 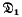is a class of groups closed under taking homomorphic images, it is easily seen that the existence of an infinite 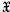-group satisfying the maximal condition for normal subgroups implies the existence of an infinite 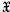-group in the class 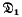, so that certain questions concerning the finiteness of groups satisfying the maximal condition for normal subgroups can be interpreted as questions about 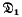-groups.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 3 , May 1971 , pp. 373 - 391
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hall, P. Nilpotent groups. Candian Math. Congress Summer Seminar. University of Alberta (1957).Google Scholar
(2)Hall, P.Wreath powers and characteristically simple groups. Proc. Cambridge Philos. Soc. 58 (1962), 170–184.CrossRefGoogle Scholar
(3)Hall, P.On non-strictly simple groups. Proc. Cambridge Philos. Soc. 59 (1963), 531–553.Google Scholar
(4)Hall, P.A note on Ī-groups. J. London Math. Soc. 39 (1964), 338–344.CrossRefGoogle Scholar
(5)Hocking, J. G. and Young, G. S.Topology (Addison-Wesley Publishing Co., Reading, Mass. 1961).Google Scholar
(6)Klingenberg, W.Linear groups over local rings. Bull. Amer. Math. Soc. 66 (1960), 294–296.CrossRefGoogle Scholar
(7)McLain, D. H.Finiteness conditions in locally soluble groups. J. London Math. Soc. 34 (1959), 101–107.CrossRefGoogle Scholar
(8)Mennicke, J. L.Finite factor groups of the unimodular group. Ann. of Math. (2), 81 (1965), 31–37.CrossRefGoogle Scholar
(9)Robinson, D. S.Joins of subnormal subgroups. Illinois J. Math. 9 (1965), 144–168.Google Scholar
(10)Roseblade, J. E.A note on disjoint subnormal subgroups. Bull. London Math. Soc. 1 (1969), 65–69.Google Scholar
(11)Szász, G.Introduction to lattice theory, 3rd edition (Academic Press; New York and London, 1963).Google Scholar
(12)Wilson, J. S.Some properties of groups inherited by normal subgroups of finite index. Math. Z. 114 (1970), 19–21.CrossRefGoogle Scholar
(13)Wilson, J. S.Groups satisfying the maximal condition for normal subgroups. Math. Z. 118 (1970), 107–114.CrossRefGoogle Scholar
(14)Wilson, J. S. The subnormal structure of general linear groups, to appear.Google Scholar