Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T02:41:05.465Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric properties of projective manifolds of small degree

Published online by Cambridge University Press:  02 December 2015

SIJONG KWAK  and
JINHYUNG PARK
SIJONG KWAK
Affiliation:
Department of Mathematical Sciences, KAIST, Daejeon, Korea. e-mail: [email protected]
JINHYUNG PARK
Affiliation:
Department of Mathematical Sciences, KAIST, Daejeon, Korea. Current address: School of Mathematics, Korea Institute for Advanced Study, Seoul, Korea. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to study geometric properties of non-degenerate smooth projective varieties of small degree from a birational point of view. First, using the positivity property of double point divisors and the adjunction mappings, we classify smooth projective varieties in 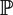$\mathbb{P}$r of degree d ⩽ r + 2, and consequently, we show that such varieties are simply connected and rationally connected except in a few cases. This is a generalisation of P. Ionescu's work. We also show the finite generation of Cox rings of smooth projective varieties in 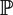$\mathbb{P}$r of degree d ⩽ r with counterexamples for d = r + 1, r + 2. On the other hand, we prove that a non-uniruled smooth projective variety in 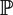$\mathbb{P}$r of dimension n and degree d ⩽ n(r − n) + 2 is Calabi–Yau, and give an example that shows this bound is also sharp.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 2 , March 2016 , pp. 257 - 277
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AHL]Artebani, M., Hausen, J. and Laface, A.On Cox rings of K3 surfaces. Composition Math. 146 (2010), 964–998.CrossRefGoogle Scholar
[BS]Beltrametti, M. C. and Sommese, A. J.The adjunction theory of complex projective varieties, de Gruyter Expositions in Mathematics 16Walter de Gruyter and Co., Berlin, (1995).CrossRefGoogle Scholar
[BCHM]Birkar, C., Cascini, P., Hacon, C. and McKernan, J.Existence of minimal models for varieties of log general type. J. Amer. Math. Soc. 23 (2010), 405–468.CrossRefGoogle Scholar
[Bui]Buium, A.On surfaces of degree at most 2n + 1 in ${\mathbb{P}}$n in Algebraic Geometry (Bucharest 1982), Lecture Notes in Math. 1056 (Springer-Verlag, Berlin, 1984), 47–67.Google Scholar
[But]Butler, D. C.Normal generation of vector bundles over a curve. J. Differential Geom. 39 (1994), 1–34.CrossRefGoogle Scholar
[E]Ein, L.Nondegenerate surfaces of degree n + 3 in ${\mathbb{P}}_{\mathbb{C}}^n$. J. Reine Angew. Math. 351 (1984), 1–11.Google Scholar
[EH]Eisenbud, D. and Harris, J.On varieties of minimal degree (a centennial account) In Algebraic geometry, Bowdoin (Brunswick, Maine, 1985), Proc. Sympos. Pure Math. 46 (1987), Part 1 (Amer. Math. Soc., Providence, RI), 3–13.Google Scholar
[FL]Fania, M. L. and Livorni, E. L.Degree nine manifolds of dimension greater than or equal to 3. Math. Nachr. 169 (1994), 117–134.CrossRefGoogle Scholar
[F1]Fujita, T.On the structure of polarized manifolds with total deficiency one I. J. Math. Soc. Japan 32 (1980), 709–725.CrossRefGoogle Scholar
[F2]Fujita, T.On the structure of polarized manifolds with total deficiency one II. J. Math. Soc. Japan 33 (1981), 415–434.CrossRefGoogle Scholar
[Fu]Fukuma, Y.On the sectional geometric genus of quasi-polarized varieties. II. Manuscripta Math. 113 (2004), 211–237.CrossRefGoogle Scholar
[GHS]Graber, T., Harris, J. and Starr, J.Families of rationally connected varieties. J. Amer. Math. Soc. 16 (2003), 57–67.CrossRefGoogle Scholar
[HM]Hacon, C. and McKernan, J.On Shokurov's rational connectedness conjecture. Duke. Math. J. 138 (2007), 119–136.CrossRefGoogle Scholar
[Hr]Harris, J.A bound on the geometric genus of projective varieties. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 8 (1981), 35–68.Google Scholar
[Ht]Hartshorne, R.Varieties of small codimension in projective space. Bull. Amer. Math. Soc. 80 (1974), 1017–1032.CrossRefGoogle Scholar
[HK]Hu, Y. and Keel, S.Mori dream spaces and GIT. Michigan Math. J. 48 (2000), 331–348.CrossRefGoogle Scholar
[II]Ilic, B.Geometric properties of the double-point divisor. Trans. Amer. Math. Soc. 350 (1998), 1643–1661.CrossRefGoogle Scholar
[Io1]Ionescu, P.Embedded projective varieties of small invariants. In Algebraic Geometry (Bucharest 1982), Lecture Notes in Math. 1056 (Springer-Verlag, Berlin, 1984), 142–186.Google Scholar
[Io2]Ionescu, P.On varieties whose degree is small with respect to codimension. Math. Ann. 271 (1985), 339–348.CrossRefGoogle Scholar
[Io3]Ionescu, P.Embedded projective varieties of small invariants III. In Algebraic Geometry (L'Aquila 1988), Lecture Notes in Math. 1417 (Springer-Verlag, Berlin, 1990), 138–154.CrossRefGoogle Scholar
[Io4]Ionescu, P.On manifolds of small degree. Comment. Math. Helv. 83 (2008), 927–940.CrossRefGoogle Scholar
[IT1]Ionescu, P. and Toma, M.Boundedness for some special families of embedded manifolds. Contemp. Math. 162 (1994), 215–225.CrossRefGoogle Scholar
[IT2]Ionescu, P. and Toma, M.On very ample vector bundles on curves. Internat. J. Math. 8 (1997), 633–643.CrossRefGoogle Scholar
[IP]Iskovskikh, V. A. and Prokhorov, Y. G.Algebraic geometry V: Fano varieties. Encyclopaedia Math. Sci. 47 (Springer, Berlin, 1999).Google Scholar
[It]Ito, A.Examples of Mori dream spaces with Picard number two. Manuscripta Math. 145 (2014), 243–254.CrossRefGoogle Scholar
[KM]Kollár, J. and Mori, S.Birational geometry of algebraic varieties. Cambridge Tracts in Math. 134 (Cambridge University Press, Cambridge 1998).Google Scholar
[LN]Lanteri, A. and Novelli, C.Ample vector bundles of small Δ-genera. J. Algebra 323 (2010), 671–697.CrossRefGoogle Scholar
[L1]Lazarsfeld, R.Positivity in algebraic geometry I. Classical Setting: line bundles and linear series. A Series of Modern Surveys in Math. 48 (Springer-Verlag, Berlin, 2004).Google Scholar
[L2]Lazarsfeld, R.Positivity in algebraic geometry II. Positivity for vector bundles, and multiplier ideals, A Series of Modern Surveys in Math. 49 (Springer-Verlag, Berlin, 2004).CrossRefGoogle Scholar
[Me]Mella, M.#-Minimal models of uniruled 3-folds. Math. Z. 242 (2002), 687–707.CrossRefGoogle Scholar
[MM]Mori, S. and Mukai, S.Classification of Fano 3-folds with B 2 ⩾ 2. Manuscripta Math. 36 (1981), 147–162. See also Erratum: “Classification of Fano 3-folds with B 2 ⩾ 2”. Manuscripta Math. 110 (2003), 407.CrossRefGoogle Scholar
[Mu]Mukai, S.Biregular classification of Fano 3-folds and Fano manifolds of coindex 3. Proc. Nat. Acad. Sci. U.S.A. 86 (1989), 3000–3002.CrossRefGoogle ScholarPubMed
[N]Noma, A.Generic inner projections of projective varieties and an application to the positivity of double point divisors. Trans. Amer. Math. Soc. 336 (2014), 4603–4623.CrossRefGoogle Scholar
[Og]Oguiso, K.Quartic K3 surfaces and Cremona transformations. In Arithmetic and Geometry of K3 Surfaces and Calabi–Yau Threefolds (Laza, R.et al. (eds.)). Fields Institue Communications 67 (Springer-Verlag, Berlin, 2013).Google Scholar
[Ot]Ottaviani, G.On 3-folds in ${\mathbb{P}}$5 which are scrolls. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 19 (1992), 451–471.Google Scholar
[TVAV]Testa, D., Várilly-Alvarado, A. and Velasco, M.Big rational surfaces. Math. Ann. 351 (2011), 95–107.CrossRefGoogle Scholar
[W1]Wiśniewski, J.On a conjecture of Mukai. Manuscripta Math. 68 (1990), 135–141.CrossRefGoogle Scholar
[W2]Wiśniewski, J.Fano 4-folds of index 2 with b 2 ⩾ 2. A contribution to Mukai classification. Bull. Polish Acad. Sci. Math. 38 (1990), 173–184.Google Scholar
[Z]Zak, F. L.Castelnuovo bounds for higher-dimensional varieties. Composoition Math. 148 (2012), 1085–1132.CrossRefGoogle Scholar