Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T16:08:10.059Z Has data issue: false hasContentIssue false
  • English
  • Français

Generators for certain normal subgroups of (2,3,7)

Published online by Cambridge University Press:  24 October 2008

John Leech
John Leech
Affiliation:
University of Glasgow
Get access Rights & Permissions [Opens in a new window]

Extract

The infinite group

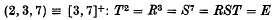
is the group of direct symmetry operations of the tessellation {3,7} of the hyperbolic plane ((3), chapter 5). This has the smallest fundamental region of any such tessellation, and related to this property is the fact that the group (2, 3, 7) has a remarkable wealth of interesting finite factor groups, corresponding to the finite maps obtained by identifying the results of suitable translations in the hyperbolic plane. The simplest example of this is the group LF(2,7), which is Klein's simple group of order 168. I have studied this group in an earlier paper ((4)), showing inter alia that the group is obtained as a factor group of (2,3,7) by adjoining any one of the relations

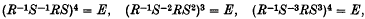
each of which implies the others. The method used was to find a set of generators for the normal subgroup with quotient group LF(2,7) and, working entirely within this subgroup, to exhibit that any one of these relations implies its collapse. The technique of working with this subgroup had been developed earlier and applied in (6) to prove that the factor group

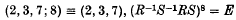
is finite and of order 10,752.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 2 , April 1965 , pp. 321 - 332
Copyright
Copyright © Cambridge Philosophical Society 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Coxeter, H. S. M.The abstract groups Gm.n.p.. Trans. Amer. Math. Soc. 45 (1939), 73–150.Google Scholar
(2)Coxeter, H. S. M.The abstract group G3.7.16. Proc. Edinburgh Math. Soc. (2), 13 (1962), 47–61.CrossRefGoogle Scholar
(3)Coxeter, H. S. M. and Moser, W. O. J.Generators and relations for discrete groups (Springer, Berlin; 1st ed. 1957, 2nd ed. 1965).CrossRefGoogle Scholar
(4)Leech, John. Some definitions of Klein's simple group of order 168 and other groups. Proc. Glasgow Math. Assoc. 5 (1962), 166–175.CrossRefGoogle Scholar
(5)Leech, John. Coset enumeration on digital computers. Proc. Cambridge Philos. Soc. 59 (1963), 257–267.CrossRefGoogle Scholar
(6)Leech, John and Mennicke, Jens. Note on a conjecture of Coxeter. Proc. Glasgow Math. Assoc. 5 (1961), 25–29.CrossRefGoogle Scholar
(7)Mendelsohn, N. S.An algorithmic solution for a problem in group theory. Canad. J. Math. 16 (1964), 509–516.CrossRefGoogle Scholar
(8)Sims, C. C.On the group (2, 3, 7; 9). Amer. Math. Soc. Notices, 11 (1964), 687–688.Google Scholar
(9)Sinkov, A.Necessary and sufficient conditions for generating certain simple groups by two operators of periods two and three. Amer. J. Math. 59 (1937), 67–76.CrossRefGoogle Scholar
(10)Sinkov, A.On the group-defining relations (2, 3, 7; p). Ann. of Math. 38 (1937), 577–584.CrossRefGoogle Scholar
(11)Todd, J. A. and Coxeter, H. S. M.A practical method for enumerating cosets of a finite abstract group. Proc. Edinburgh Math. Soc. (2), 5 (1936), 26–34.CrossRefGoogle Scholar