Generalized Bianchi identities for horizontal distributions
Published online by Cambridge University Press: 24 October 2008
Extract
A linear connection on a differentiable manifold M defines a horizontal distribution on the tangent bundle T(M). Horizontal distributions on tangent bundles are of some interest even when they are not generated by connections. Much of linear connection theory generalizes to arbitrary horizontal distributions. In particular, there are generalized versions of Bianchi's two identities for the torsion T and curvature R
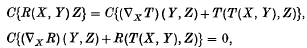
where C denotes the cyclic sum with respect to X, Y and Z. These identities are derived below by associating with a horizontal distribution a graded derivation of degree 1 in a graded Lie algebra of vertical forms on M. This approach reveals the fundamentally algebraic origin of the Bianchi identities.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 1 , July 1983 , pp. 125 - 132
- Copyright
- Copyright © Cambridge Philosophical Society 1983
References
REFERENCES
- 10
- Cited by


