Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T02:48:57.918Z Has data issue: false hasContentIssue false
  • English
  • Français

General series involving H-functions

Published online by Cambridge University Press:  24 October 2008

R. N. Jain
R. N. Jain
Affiliation:
Holkar Science College, Indore (M.P.), India
Get access Rights & Permissions [Opens in a new window]

Extract

MacRobert (4–7) and Ragab(8) have summed many infinite and finite series of E-functions by expressing the E-functions as Barnes integrals and interchanging the order of summation and integration. Verma (9) has given two general expansions involving E-functions from which, in addition to some new results, all the expansions given by MacRobert and Ragab can be deduced. Proceeding similarly, we have studied general summations involving H-functions. The H-function is the most generalized form of the hypergeometric function. It contains a vast number of well-known analytic functions as special cases and also an important class of symmetrical Fourier kernels of a very general nature. The H-function is defined as (2)

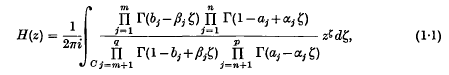
where 0 ≤ n ≤ p, 1 ≤ m ≤ q, αj, βj are positive numbers and aj, bj may be complex numbers.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 2 , March 1969 , pp. 461 - 465
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bailey, W. N.Generalized Hypergeometric Series (Cambridge, 1935).Google Scholar
(2)Braaksma, B. L. J.Asymptotic expansions and analytic continuations for a class of Barnes-integrals. Compositio Math. 15 (1964), 239–342.Google Scholar
(3)Carlitz, L.Summation of a special 4F 3. Boll. Un. Mat. Ital. (3), 18 (1963), 90–93.Google Scholar
(4)MacRoberts, T. M.Infinite series of E-functions. Proc. Glasgow Math. Assoc. 4 (1958), 26–28.CrossRefGoogle Scholar
(5)MacRobert, T. M.The multiplication formula for the gamma function and E-function series. Math. Ann. 139 (1959), 133–139.CrossRefGoogle Scholar
(6)MacRobert, T. M.Infinite series of E-functions, Math. Z. 71 (1959), 143–145.CrossRefGoogle Scholar
(7)MacRobert, T. M.Application of the multiplication formula for the gamma functions to E-functions. Proc. Glasgow Math. Assoc. 5 (1960), 114–118.CrossRefGoogle Scholar
(8)Ragab, F. M.Infinite series of E-functions. Math. Ann. 148 (1962), 94–97.CrossRefGoogle Scholar
(9)Verma, A.General expansions involving E-functions. Math. Z. 83 (1964), 29–36.CrossRefGoogle Scholar