Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T14:01:17.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Further aspects of the evaluation of σ(m. n≠0, 0) (am2 + bnm + cn2)−s

Published online by Cambridge University Press:  24 October 2008

I. J. Zucker  and
M. M. Robertson
I. J. Zucker
Affiliation:
Department of Physics, University of Surrey, Guildford
M. M. Robertson
Affiliation:
Department of Mathematics, University of Surrey, Guildford
Get access Rights & Permissions [Opens in a new window]

Extract

In some previous publications, Zucker and Robertson [13, 14, 15] for certain cases evaluated exactly the double sum

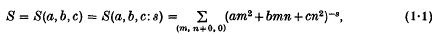
with a, b, c integers. In (1·1) the summation is over all integer values of m and n, both positive and negative, but excluding the case where m and n are simultaneously zero. The term ‘exact’ used here is in the sense introduced by Glasser [5], and means that S may be expressed as a linear sum of products of pairs of Dirichlet L-series. S is then said to be solvable. Whether S may be solved or not depends on the properties of the related binary quadratic form (am2 + bmn + cn2) = (a, b, c). The cases considered in [15] were when a > 0 and d = b2 − 4ac < 0, i.e. (a, b, c) was positive definite. When this is so, Glasser [5] conjectured that S was solvable if and only if (a, b, c) had one reduced form per genus, i.e. the reduced forms of (a, b, c) were disjoint. Zucker and Robertson [15] were in fact able to solve S for all (a, b, c) for which d < 0 and whose reduced forms were disjoint. A complete list of solutions may be found in [6].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 1 , January 1984 , pp. 5 - 13
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baker, A. and Schinzel, A.. On the least integers represented by the genera of binary quadratic forms. Acta Arith. 18 (1971), 137–144.CrossRefGoogle Scholar
[2] Berndt, B. C.. A double summation. SIAM Rev. 16 (1974), 555–557.CrossRefGoogle Scholar
[3] Chowla, S.. An extension of Heilbrom's class number theorem. Quart. J. Math. Oxford Ser. 5 (1934), 304–307.CrossRefGoogle Scholar
[4] Durell, C. V. and Robson, A.. Advanced Trigonometry, ch. ix and xii (G. Bell, 1967).Google Scholar
[5] Glasser, M. L.. The evaluation of lattice sums. II. Number theoretic approach. J. Math. Phys. 14 (1973), 701–703.CrossRefGoogle Scholar
[6] Glasser, M. L. and Zucker, I. J.. Lattice sums. Theoret. Chem. Adv. & Perspectives 5 (1980), 67–139.CrossRefGoogle Scholar
[7] Grosswald, E.. Negative discriminants of binary quadratic forms with one class in each genus. Acta Arith. 8 (1963), 295–306.CrossRefGoogle Scholar
[8] Lorenz, L.. Bidrag til tallenes theori. Tidsskrift for Math. 1 (1871), 97–114.Google Scholar
[9] Selberg, A. and Chowla, S.. On Epstein's zeta-function. J. reine angew. Math. 227 (1967), 86–110.Google Scholar
[10] Siegel, C. L.. Advanced Analytic Number Theory, vol. 62 (Tata Institute, 1980).Google Scholar
[11] Whittaker, E. T. and Watson, G. N.. Modern Analysis, 4th edn., ch. xiii (C.U.P., 1927).Google Scholar
[12] Zucker, I. J.. The evaluation in terms of Γ-functions of the periods of elliptic curves admitting complex multiplication. Math. Proc. Cambridge Philos. Soc. 82 (1977), 111–118.CrossRefGoogle Scholar
[13] Zucker, I. J. and Robertson, M. M.. Exact values for some two dimensional lattice sums. J. Phys. A 8 (1975), 874–881.Google Scholar
[14] Zucker, I. J. and Robertson, M. M.. Some properties of Dirichlet L-series. J. Phys. A 9 (1976), 1207–1214.CrossRefGoogle Scholar
[15] Zucker, I. J. and Robertson, M. M.. A systematic approach to the evaluation of Σ(m n≠0,0) (am2+bmn+cn2)−s. J. Phys. A 9 (1976), 1215–1224.Google Scholar