Functions regular in the unit circle
Published online by Cambridge University Press: 24 October 2008
Extract
Let
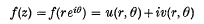
be a function regular for | z | < 1. With the hypotheses f(0) = 0 and
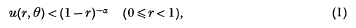
for some positive constant α, Cartwright(1) has deduced upper bounds for |f(z) | in the unit circle. Three cases have arisen and according as (1) holds with α < 1, α = 1 or α > 1, the bounds on each circle | z | = r are given respectively by
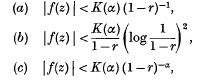
K(α) being a constant which depends only on the corresponding value of α which occurs in (1). We shall always use the symbols K and A to represent constants dependent on certain parameters such as α, not necessarily having the same value at each occurrence.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 52 , Issue 1 , January 1956 , pp. 49 - 60
- Copyright
- Copyright © Cambridge Philosophical Society 1956
References
REFERENCES
- 6
- Cited by


