Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T01:58:07.755Z Has data issue: false hasContentIssue false
  • English
  • Français

Free subgroups of certain one-relator groups defined by positive words

Published online by Cambridge University Press:  24 October 2008

Gilbert Baumslag
Gilbert Baumslag
Affiliation:
City College of C.U.N.Y., New York
Get access Rights & Permissions [Opens in a new window]

Extract

Let ℒ be the class of those groups G which can be presented in the form

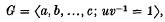
where u and v are positive words in the given generators. Here a word w is termed positive if only non-negative powers of a, b,…, c occur in w. If each generator occurs with exponent sum zero in uv-1, we term the ℒ-group G a 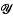-group. This class 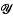contains, in particular, the class X of those groups G which can be presented in the form

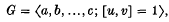
where u and v are positive words, and where [u, v] is the commutator uvu-1v-1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 2 , March 1983 , pp. 247 - 251
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baumslag, G.On generalised free products. Math. Z. 78 (1962), 423–438.CrossRefGoogle Scholar
(2)Baumslag, G.On the residual finiteness of generalised free products of nilpotent groups. Trans. Amer. Math. Soc. 106 (1963), 193–209.CrossRefGoogle Scholar
(3)Baumslag, G.Positive one-relator groups. Trans. Amer. Math. Soc. 156 (1971), 165–183.CrossRefGoogle Scholar
(4)Baumslag, G., Dyer, E. and Heller, A.The topology of discrete groups. J. Pure and Appl. Algebra, 16 (1980), 1–47.CrossRefGoogle Scholar
(5)Frederick, K. N.The hopfian property for a class of fundamental groups. Comm. Pure Appl. Math. 16 (1963), 1–8.CrossRefGoogle Scholar
(6)Karrass, A. and Solitar, D.The subgroups of a free product of two groups with an amalgamated subgroup. Trans. Amer. Math. Soc. 144 (1970), 227–255.CrossRefGoogle Scholar
(7)Lyndon, R. C. and Schupp, P. E.Combinatorial Group Theory (Ergebnisse der Math. 89, Springer-Verlag, Berlin, Heidelberg, New York, 1977).Google Scholar
(8)Magnus, W.Uber diskontinuierliche Gruppen mit einer definierenden Relation (Der Freiheitssatz). J. Reine Angew. Math. 163 (1930), 141–165.CrossRefGoogle Scholar
(9)Magnus, W.Das Identitatsproblem fur Gruppen mit einer definierenden Relation. Math Annalen, 106 (1932), 295–307.CrossRefGoogle Scholar
(10)Magnus, W.Beziehungen zwischen Gruppen und Idealen in einem speziellen Ring. Math. Annalen, 111 (1935), 259–280.CrossRefGoogle Scholar
(11)Magnus, W.Uber freie Faktorgruppen und freie Untergruppen gegebener Gruppen. Monatsh. Math. 47 (1939), 105–115.CrossRefGoogle Scholar
(12)Magnus, W., Karrass, A. and Solitar, D.Combinatorial Group Theory (Wiley Publishing Co., New York, 1966).Google Scholar
(13)Wicks, M. J.Commutators in free products. J. London Math. Soc. 37 (1962), 433–444.CrossRefGoogle Scholar