Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T14:08:46.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Fitting functors in finite solvable groups: II

Published online by Cambridge University Press:  24 October 2008

James C. Beidleman ,
Ben Brewster  and
Peter Hauck
James C. Beidleman
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY 40506, U.S.A.
Ben Brewster
Affiliation:
Department of Mathematical Sciences, State University of New York, Binghamton, NY 13901, U.S.A.
Peter Hauck
Affiliation:
Mathematisches Institut, Albert-Ludwigs-Universität, D 7800 Freiburg, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a continuation of [1], where we introduced the concept and investigated the basic properties of Fitting functors for finite solvable groups. We recall that a map f which assigns to each finite solvable group G a non-empty set f(G) of subgroups of G is called a Fitting functor if the following property is satisfied: whenever α: G → H is a monomorphism with α(G) ⊴ H, then

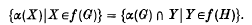
The most prominent examples of conjugate Fitting functors are provided by injectors of Fitting classes. However, Fitting functors f in general do not behave as nicely as injectors. For instance, f(G) need not consist of pronormal subgroups of a group G (cf. [1], 4·3).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 1 , January 1987 , pp. 37 - 55
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beidleman, J. C., Brewster, B. and Hauck, P.. Fittingfunktoren in endlichen auflösbaren Gruppen I. Math. Z. 182 (1983), 359–384.CrossRefGoogle Scholar
[2]Brison, O. J.. Hall operators for Fitting classes. Arch. Math. 33 (1979), 1–9.CrossRefGoogle Scholar
[3]Doerk, K. and Porta, M.. Über Vertauschbarkeit, normale Einbettung und Dominanz bei Fittingklassen endlicher auflösbarer Gruppen. Arch. Math. 35 (1980), 319–327.CrossRefGoogle Scholar
[4]Hartley., B.On Fischer's dualization of formation theory. Proc. London Math. Soc. (3) 19 (1969), 193–207.CrossRefGoogle Scholar
[5]Hauck., P.On products of Fitting classes. J. London Math. Soc. (2) 20 (1979), 423–434.CrossRefGoogle Scholar
[6]Lockett., F. P. On the theory of Fitting classes of finite soluble groups. Ph.D. thesis, University of Warwick (1971).Google Scholar
[7]Lockett., F. P.The Fitting class . Math. Z. 137 (1974), 131–136.CrossRefGoogle Scholar