Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Marar, W.L.
and
Nuño-Ballesteros, J.J.
2009.
The doodle of a finitely determined map germ from R2 to R3.
Advances in Mathematics,
Vol. 221,
Issue. 4,
p.
1281.
Grulha, Nivaldo G.
Hernandes, Marcelo E.
and
Martins, Rodrigo
2012.
Polar multiplicities and Euler obstruction for ruled surfaces.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 43,
Issue. 3,
p.
443.
Barbosa, Grazielle Feliciani
Martins, Rodrigo
and
Saia, Marcelo José
2012.
Topology of simple singularities of ruled surfaces in Rp.
Topology and its Applications,
Vol. 159,
Issue. 2,
p.
397.
Moya-Pérez, J. A.
and
Nuño-Ballesteros, J. J.
2014.
Topological classification of corank 1 map germs from $$\mathbb {R}^{3}$$ R 3 to $$\mathbb {R}^{3}$$ R 3.
Revista Matemática Complutense,
Vol. 27,
Issue. 2,
p.
421.
Nuño-Ballesteros, J. J.
2018.
Singularities and Foliations. Geometry, Topology and Applications.
Vol. 222,
Issue. ,
p.
3.
HERNANDES, M.E.
MARTINS, R.
and
RODRIGUES HERNANDES, M.E.
2018.
On the polar varieties of ruled hypersurfaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 164,
Issue. 2,
p.
193.
Moya-Pérez, J. A.
and
Nuño-Ballesteros, J. J.
2022.
Double points in families of map germs from ℝ2 to ℝ3.
Journal of Topology and Analysis,
Vol. 14,
Issue. 01,
p.
93.
Moya-Pérez, J.A.
and
Nuño-Ballesteros, J.J.
2023.
The dual tree of a fold map germ from to .
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 153,
Issue. 3,
p.
958.
ALTINKAYA, Anıl
and
ÇALIŞKAN, Mustafa
2023.
B-Lift curves and its ruled surfaces.
Communications Faculty Of Science University of Ankara Series A1Mathematics and Statistics,
Vol. 72,
Issue. 1,
p.
159.


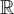
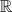
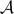 -equivalent to a ruled surface. Moreover, we give a topological classification of
-equivalent to a ruled surface. Moreover, we give a topological classification of 