Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T15:12:15.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of polynomials defined on subspaces

Published online by Cambridge University Press:  16 March 2010

MAITE FERNÁNDEZ-UNZUETA  and
ÁNGELES PRIETO
MAITE FERNÁNDEZ-UNZUETA
Affiliation:
Centro de Investigación en Matemáticas (CIMAT), A.P. 402, Guanajuato, 36000, Gto., Mexico. e-mail: [email protected]
ÁNGELES PRIETO
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, Spain. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k ∈ ℕ and let E be a Banach space such that every k-homogeneous polynomial defined on a subspace of E has an extension to E. We prove that every norm one k-homogeneous polynomial, defined on a subspace, has an extension with a uniformly bounded norm. The analogous result for holomorphic functions of bounded type is obtained. We also prove that given an arbitrary subspace F ⊂ E, there exists a continuous morphism φk, F: 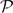(kF) → 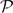(kE) satisfying φk, F(P)|F = P, if and only E is isomorphic to a Hilbert space.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 3 , May 2010 , pp. 505 - 518
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aron, R. M. and Berner, P. D.A Hahn–Banach extension theorem for analytic mappings. Bull. Soc. Math. France 106 (1978), no. 1, 3–24.CrossRefGoogle Scholar
[2]Aron, R. M., Boyd, C. and Choi, Y. S.Unique Hahn–Banach Theorems for spaces of homogeneous polynomials. J. Aust. Math. Soc. 70 (2001), no. 3, 387–400.CrossRefGoogle Scholar
[3]Aron, R. M. and Schottenloher, M.Compact holomorphic mappings on Banach spaces and the approximation theory. J. Funct. Anal. 21 (1976), 7–30.CrossRefGoogle Scholar
[4]Bennett, G., Dor, L. E., Goodman, V., Johnson, W. B. and Newman, C. M.On uncomplemented subspaces of L p, 1 < p < 2. Israel J. Math. 26 (1977), no. 2, 178–187.CrossRefGoogle Scholar
[5]Bourgain, J.A counterexample to a complementation problem. Compositio Math. 43 (1981), no. 1, 133–144.Google Scholar
[6]Carando, D.Extendible polynomials on Banach spaces. J. Math. Anal. Math. Appl. 233 (1999), 359–372.CrossRefGoogle Scholar
[7]Casazza, P. G. and Nielsen, N. J.The Maurey extension property for Banach spaces with the Gordon-Lewis property and related structures. Studia Math. 155 (2003), no. 1, 1–21.CrossRefGoogle Scholar
[8]Castillo, J. M. F., Defant, A., García, R., Pérez-García, D. and Suárez, J. Local complementation and the extension of bilinear mappings, preprint.Google Scholar
[9]Diestel, J., Jarchow, H. and Tonge, A.Absolutely summing operators Cambridge Studies in Advanced Mathematics, 43. (Cambridge University Press, 1995).CrossRefGoogle Scholar
[10]Davis, W. J., Dean, D. W. and Singer, I.Complemented subspaces and Λ systems in Banach spaces. Israel. J. Math. 6 (1968), 303–309.CrossRefGoogle Scholar
[11]Dineen, S. Holomorphically complete locally convex topological vector spaces. Lecture Notes in Math. 332. (Springer, 1973), 77–111.Google Scholar
[12]Dineen, S.Complex analysis on infinite dimensional spaces. Springer Monographs in Mathematics (Springer, 1999).CrossRefGoogle Scholar
[13]Fakhoury, H.Sélections linéaires associées au théorème de Hahn–Banach. J. Funct. Anal. 11 (1972), 436–452.CrossRefGoogle Scholar
[14]Figiel, T., Lindenstrauss, J. and Milman, V. D.The dimension of almost spherical sections of convex bodies. Acta Math. 139 (1977), no. 1-2, 53–94.CrossRefGoogle Scholar
[15]Galindo, P., García, D., Maestre, M. and Mujica, J.Extension of multilinear mappings on Banach spaces. Studia Math. 108 (1994), no. 1, 55–76.CrossRefGoogle Scholar
[16]Garling, D. J. H. and Gordon, Y.Relations between some constants associated with finite dimensional Banach spaces. Israel J. Math. 9 (1971), 346–361.CrossRefGoogle Scholar
[17]Jarchow, H., Palazuelos, C., Pérez-García, D. and Villanueva, I.Hahn–Banach extension of multilinear forms and summability. J. Math. Anal. Appl. 336 (2007), no. 2, 1161–1177.CrossRefGoogle Scholar
[18]Kirwan, P. and Ryan, R.Extendibility of homogeneous polynomials on Banach spaces. Proc. Amer. Math. Soc. 126 (4) (1998), 1023–1029.CrossRefGoogle Scholar
[19]Lindenstrauss, J. and Tzafriri, L.On the complemented subspaces problem. Israel. J. Math. 9 (1971), 263–269.CrossRefGoogle Scholar
[20]Lindenstrauss, J. and Tzafriri, L.Classical Banach spaces. I. Sequence spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, Vol. 92 (Springer-Verlag, 1977).Google Scholar
[21]Maurey, B.Un Théorème de prolongement. C. R. Acad. Sci. Paris Sér. A 279 (1974), 329–332.Google Scholar
[22]Mujica, J.Complex analysis in Banach spaces. Holomorphic functions and domains of holomorphy in finite and infinite dimensions. North-Holland Mathematics Studies, 120. (North-Holland Publishing Co., 1986).Google Scholar
[23]Pełczyński, A.On weakly compact polynomial operators on B-spaces with Dunford-Pettis property. Bull. Acad. Polon. Sci. Sr. Sci. Math. Astronom. Phys. 11 (1963), 371–378.Google Scholar
[24]Pietsch, A.History of Banach spaces and linear operators (Birkhäuser Boston, Inc., 2007).Google Scholar
[25]Rosenthal, H. P.On the subspaces of L p (p > 2) spanned by sequences of independent random variables. Israel J. Math. 8 (1970), 273–303.CrossRefGoogle Scholar
[26]Zalduendo, I.Extending polynomials on Banach spaces–a survey. Rev. Un. Mat. Argentina 46 (2005), no. 2, 45–72.Google Scholar