Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T02:33:47.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of a theorem of C. G. F. James

Published online by Cambridge University Press:  24 October 2008

D. W. Babbage
D. W. Babbage
Affiliation:
Magdalene College
Get access Rights & Permissions [Opens in a new window]

Extract

The linear subspaces [k] of a space [n] have been represented by Grassmann by the points of a rational locus V(n−k)(k+1), of dimension (n−k)(k+1), in 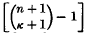; the representation is effected by taking as independent homogeneous coordinates of a [k] in [n] the 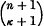determinants of order k+1 which belong to the matrix, of k+1 rows and n+1 columns, formed by the co-ordinates of any k+1 linearly independent points of the [k].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 28 , Issue 4 , October 1932 , pp. 421 - 426
Copyright
Copyright © Cambridge Philosophical Society 1932

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See Segre, , Encyk. der Math. Wiss., iii C 7, p. 791.Google Scholar

† Brown, L. M., Journal Lond. Math. Soc., 5 (1930), 168–176.CrossRefGoogle Scholar

‡ A [k] is said to be chordal to a given curve when it meets it in k + 1 points.

§ James, C. G. F., Proc. Camb. Phil. Soc., 21 (1923), 664.Google Scholar

* This theorem has been given by MissTelling, H. G., Proc. Camb. Phil. Soc., 28 (1932), 403–415.CrossRefGoogle Scholar