Estimates of Zeros of a Polynomial
Published online by Cambridge University Press: 24 October 2008
Extract
Throughout this note we shall consider a fixed polynomial 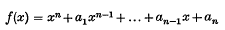 with complex coefficients and of degree n ≥ 2. Its zeros will be denoted by ξ1, ξ2, …, ξn where the numbering is such that
with complex coefficients and of degree n ≥ 2. Its zeros will be denoted by ξ1, ξ2, …, ξn where the numbering is such that 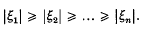 Making use of Jensen's integral formula, Mahler (4) showed that, for l ≥ k < n,
Making use of Jensen's integral formula, Mahler (4) showed that, for l ≥ k < n, 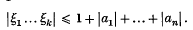 A slightly weaker result had been established by Feldman in an earlier publication (2). Mahler's inequality (1) is of importance in the study of transcendental numbers, and our first object is to sharpen his bound by proving the following result.
A slightly weaker result had been established by Feldman in an earlier publication (2). Mahler's inequality (1) is of importance in the study of transcendental numbers, and our first object is to sharpen his bound by proving the following result.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 229 - 234
- Copyright
- Copyright © Cambridge Philosophical Society 1962
References
REFERENCES
- 4
- Cited by


