Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T17:10:40.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Essential geometric morphisms between toposes over finite sets

Published online by Cambridge University Press:  24 October 2008

John Haigh
John Haigh
Affiliation:
University of Durham
Get access Rights & Permissions [Opens in a new window]

Extract

We show that if {Gi}J ε I is a generating set for an (elementary) topos ℰ then {P(Gi)}iεI is a cogenerating set for x2130;. From this we show that if topos ℰ contains an object G whose subobjects generate ℰ, then ΩG is a cogenerator for ℰ. Let 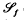denote the topos of finite sets and functions. We also show that if ℰ1 is a topos and ℰ2 is a bounded 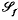-topos then every geometric morphism ℰ1 → ℰ2 is essential.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 1 , January 1980 , pp. 21 - 24
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Borceux, F.When is Ω a cogenerator in a topoos? Cahiers top. et géom. diff. 16 (1975), 3–15.Google Scholar
(2)Grothendieck, A. and Verdier, J. L.Théorie des Topos, SGA 4, exposés I–VI, Springer Lecture Notes in Mathematics, nos. 269 and 270 (1972).Google Scholar
(3)Haigh, J. Toposes over Finite Sets. D.Phil, thesis, University of Sussex (1978).Google Scholar
(4)Johnstone, P. T.Topos theory, L.M.S. Mathematical Monographs, no. 10 (Academic Press, 1977).Google Scholar
(5)Paré, R.Colimits in topoi. Bull. Amer. Math. Soc. 80 (1974), 556–561.CrossRefGoogle Scholar
(6)Wraith, G. C. Lectures on elementary topoi, Model theory and Topoi, Springer Lecture Notes in Mathematics, no. 445 (1975).Google Scholar