Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T00:41:28.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Equally Inclined Spheres

Published online by Cambridge University Press:  24 October 2008

J. G. Mauldon
J. G. Mauldon
Affiliation:
Corpus Christi CollegeOxford and University of CaliforniaBerkeley
Get access Rights & Permissions [Opens in a new window]

Extract

If five spheres in 3-space are such that each pair is inclined at the same non-zero angle θ, then 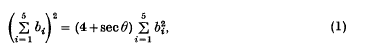where b1, …, b5 (the ‘bends’ (1) of the spheres) are the reciprocals of their radii. To prove this result, establish a system of rectangular cartesian coordinates (x, y, z) and let the spheres have centres (xi, yi, zi) and radii 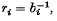, where i = 1,…, 5. Then for x5, y5, z5, r5 we have the equations 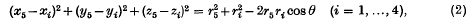which, on subtraction, yield three linear equations and one quadratic equation. Solving the three linear equations for x5, y5, z5 and substituting, we see that the required relation is algebraic (indeed quadratic) in r5 and hence in b5. Since it is also symmetric in b1,…, b5, it follows that it can be expressed as a polynomial relation in the elementary symmetric functions p1, …, p5 in b5, …, b5.

Type
Research Notes
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 420 - 421
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Soddy, F.The Kiss Precise. Nature, 137 (1936), 1021.CrossRefGoogle Scholar
(2)Coxeter, H. S. M.An introduction to geometry (New York, 1961).Google Scholar
(3)Mauldon, J. G Sets of equally inclined spheres. Canad. J. Math (to appear).Google Scholar
(4)Mauldon, J. G Bunches of cones. American Math. Monthly (to appear).Google Scholar