Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hall, R. R.
1995.
A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function.
Mathematika,
Vol. 42,
Issue. 1,
p.
144.
Hall, R. R.
1996.
Proof of a conjecture of Heath-Brown concerning quadratic residues.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 3,
p.
581.
Halberstadt, Emmanuel
and
Kraus, Alain
2002.
Courbes de Fermat: résultats et problèmes.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 548,
Granville, Andrew
and
Soundararajan, K.
2003.
Decay of Mean Values of Multiplicative Functions.
Canadian Journal of Mathematics,
Vol. 55,
Issue. 6,
p.
1191.
Matomäki, Kaisa
and
Radziwiłł, Maksym
2015.
Sign changes of Hecke eigenvalues.
Geometric and Functional Analysis,
Vol. 25,
Issue. 6,
p.
1937.
Royer, Emmanuel
Sengupta, Jyoti
and
Wu, Jie
2016.
Non-vanishing and sign changes of Hecke eigenvalues for Siegel cusp forms of genus two.
The Ramanujan Journal,
Vol. 39,
Issue. 1,
p.
179.
Chen, B.
and
Wu, J.
2016.
Non-vanishing and sign changes of Hecke eigenvalues for half-integral weight cusp forms.
Indagationes Mathematicae,
Vol. 27,
Issue. 2,
p.
488.
Tenenbaum, Gérald
2017.
Moyennes effectives de fonctions multiplicatives complexes.
The Ramanujan Journal,
Vol. 44,
Issue. 3,
p.
641.
Mangerel, Alexander P
2020.
Short Character Sums and the Pólya–Vinogradov Inequality.
The Quarterly Journal of Mathematics,
Vol. 71,
Issue. 4,
p.
1281.
Hua, Guodong
2022.
On the sign changes and non-vanishing of Hecke eigenvalues associated to symmetric power L-Functions.
The Ramanujan Journal,
Vol. 59,
Issue. 3,
p.
775.
Pollack, Paul
and
Singha Roy, Akash
2023.
Benford behavior and distribution in residue classes of large prime factors.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 2,
p.
626.
Granville, Andrew
and
Mangerel, Alexander P.
2023.
Three conjectures about character sums.
Mathematische Zeitschrift,
Vol. 305,
Issue. 3,
Pollack, Paul
and
Singha Roy, Akash
2025.
Mean values of multiplicative functions and applications to residue-class distribution.
Proceedings of the Edinburgh Mathematical Society,
p.
1.

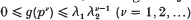 for all primes p, with constants λ1 ≥ 0, 0 ≤ λ2 < 2. Their upper bound is sharp to within a factor (l + o(l)), but even a weaker and easier to prove estimate, such as
for all primes p, with constants λ1 ≥ 0, 0 ≤ λ2 < 2. Their upper bound is sharp to within a factor (l + o(l)), but even a weaker and easier to prove estimate, such as