Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T17:22:25.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffraction by an imperfectly conducting right-angled wedge

Published online by Cambridge University Press:  24 October 2008

W. E. Williams
W. E. Williams
Affiliation:
Department of Applied MathematicsUniversity of Liverpool
Get access Rights & Permissions [Opens in a new window]

Abstract

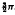A new and exact solution is given for the diffraction of the field of an electric line current by an imperfectly conducting wedge of exterior angle . Previous attempts at solving this problem assumed that the solution could be expressed as a series in inverse powers of the conductivity of the wedge, but this approach can only be applied to wedges of exterior angle less than π as the solution obtained is singular at the edge of the wedge for angles exceeding π. It is shown that in the present case no such expansion is uniformly valid; at large distances from the wedge, however, the present solution agrees with that obtained by assuming an expansion in inverse powers of the conductivity, even though this latter solution is singular at the edge, to order (conductivity of the wedge)−1; the next term in the expansion of the present exact solution is O(conductivity)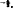. The case of an incident plane wave may be obtained by letting the source tend to infinity.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 55 , Issue 2 , April 1959 , pp. 195 - 209
Copyright
Copyright © Cambridge Philosophical Society 1959

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bromwich, T. J. I'A.Proc. Land. Math. Soc. 14 (1915), 450–63.CrossRefGoogle Scholar
(2)Carslaw, H. S.Proc. Lond. Math. Soc. 30 (1899), 121–63.Google Scholar
(3)Carslaw, H. S.Proc. Lond. Math. Soc. 18 (1920), 291–306.CrossRefGoogle Scholar
(4)Clemmow, P. C.Quart. J. Mech. Appl. Math. 3 (1950), 241–56.CrossRefGoogle Scholar
(5)Erdelyi, A.J. Soc. Industr. Appl. Math. 3 (1955), 17–27.CrossRefGoogle Scholar
(6)Felsen, L. B.Symposium on micro wave optics, vol. I. Eaton Electronics Lab. Montreal.Google Scholar
(7)Garnir, H. G.Bull. Soc. Roy. Sci. Liège, 21 (1952) 119–40, 207–31.Google Scholar
(8)Jones, D. S. and Pidduck, F. B.Quart. J. Math. 1 (1950), 229–37.CrossRefGoogle Scholar
(9)Jones, D. S.Quart. J. Mech. Appl. Math. 3 (1950), 420–34.CrossRefGoogle Scholar
(10)Jones, D. S.Proc. Camb. Phil. Soc. 49 (1953), 668–84.CrossRefGoogle Scholar
(11)Karp, S. N. and Karal, F.Research Report. E.M. 113, N.Y.U.Google Scholar
(12)Kay, A.Research Report, October 1954, Tech. Res. Gp. N. York.Google Scholar
(13)Kreysig, E.Acta Math. 85 (1951), 117–81.CrossRefGoogle Scholar
(14)Kreysig, E.Acta Math. 89 (1953), 107–31.CrossRefGoogle Scholar
(15)Macdonald, H. M.Proc. Lond. Math. Soc. 14 (1915), 410–27.CrossRefGoogle Scholar
(16)Oberhettinger, F.Commun. Pur. Appl. Math. 7 (1954), 551–63.CrossRefGoogle Scholar
(17)Oberhettinger, F.J. Math. Phys. 34 (1955), 245–55.CrossRefGoogle Scholar
(18)Reiche, F.Math. Ann. 37 (1912).Google Scholar
(19)Senior, T. B. A.Proc. Roy. Soc. A, 213 (1952), 436–58.Google Scholar
(20)Stoker, J.J. Quart. Appl. Math. 5 (1947), 1–54.CrossRefGoogle Scholar
(21)Sommerfeld, A.Math. Ann. 7 (1896), 317–41.CrossRefGoogle Scholar
(22)Williams, W. E.J. Math. Phys. 36 (1957), 26–35.CrossRefGoogle Scholar