Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elliott, Robert J.
and
Friedman, Avner
1975.
A Note on Generalized Pursuit-Evasion Games.
SIAM Journal on Control,
Vol. 13,
Issue. 1,
p.
105.
Kalton, N. J.
1975.
The Theory and Application of Differential Games.
p.
45.
Godefroy, G.
2014.
Obituary: Nigel John Kalton, 1946–2010.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 6,
p.
1292.


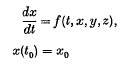
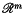 , with pay-off
, with pay-off