Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cohen, Joel E.
1979.
Ergodic theorems in demography.
Bulletin of the American Mathematical Society,
Vol. 1,
Issue. 2,
p.
275.
Cohen, Joel E.
1979.
Random evolutions and the spectral radius of a non-negative matrix.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 2,
p.
345.
Friedland, Shmuel
1981.
Convex spectral functions.
Linear and Multilinear Algebra,
Vol. 9,
Issue. 4,
p.
299.
Deutsch, Emeric
and
Neumann, Michael
1985.
On the first and second order derivatives of the Perron vector.
Linear Algebra and its Applications,
Vol. 71,
Issue. ,
p.
57.
D. Nussbaum, Roger
1986.
Convexity and log convexity for the spectral radius.
Linear Algebra and its Applications,
Vol. 73,
Issue. ,
p.
59.
Hansen, Poul Einer
1989.
Leslie matrix models.
Mathematical Population Studies,
Vol. 2,
Issue. 1,
p.
37.
Haviv, Moshe
Ritov, Ya'acov
and
Rothblum, Uriel G.
1992.
Taylor expansions of eigenvalues of perturbed matrices with applications to spectral radii of nonnegative matrices.
Linear Algebra and its Applications,
Vol. 168,
Issue. ,
p.
159.
Kirkland, Stephen J.
and
Neumann, Michael
1994.
Convexity and Concavity of the Perron Root and Vector of Leslie Matrices with Applications to a Population Model.
SIAM Journal on Matrix Analysis and Applications,
Vol. 15,
Issue. 4,
p.
1092.
Caswell, Hal
2000.
No inconsistencies in sensitivity analysis.
Trends in Ecology & Evolution,
Vol. 15,
Issue. 5,
p.
204.
MACLEAN, MAIREAD M.
CARSLAKE, DAVID J.
EVANS, MATTHEW R.
TOWNLEY, STUART
and
HODGSON, DAVID J.
2008.
The usefulness of sensitivity analysis for predicting the effects of cat predation on the population dynamics of their avian prey.
Ibis,
Vol. 150,
Issue. s1,
p.
100.
Neumann, Michael
and
Sze, Nung-Sing
2008.
A note on the perturbation of positive matrices by normal and unitary matrices.
Linear Algebra and its Applications,
Vol. 428,
Issue. 1,
p.
224.
McCarthy, Dominic
Townley, Stuart
and
Hodgson, Dave
2008.
On second order sensitivity for stage-based population projection matrix models.
Theoretical Population Biology,
Vol. 74,
Issue. 1,
p.
68.
Altenberg, Lee
2009.
The Evolutionary Reduction Principle for Linear Variation in Genetic Transmission.
Bulletin of Mathematical Biology,
Vol. 71,
Issue. 5,
p.
1264.
Carslake, David
Townley, Stuart
and
Hodgson, David J.
2009.
Predicting the impact of stage‐specific harvesting on population dynamics.
Journal of Animal Ecology,
Vol. 78,
Issue. 5,
p.
1076.
Parnes, Dror
2010.
Time to default and other sensitivities of credit ratings.
Quantitative Finance,
Vol. 10,
Issue. 9,
p.
947.
2012.
Group Inverses of M-Matrices and Their Applications.
Vol. 20121629,
Issue. ,
Rothblum, Uriel
2013.
Handbook of Linear Algebra, Second Edition.
Vol. 20134740,
Issue. ,
p.
137.
Shyu, Esther
Caswell, Hal
and
Freckleton, Robert
2014.
Calculating second derivatives of population growth rates for ecology and evolution.
Methods in Ecology and Evolution,
Vol. 5,
Issue. 5,
p.
473.
Xu, Jianhong
2015.
An iterative algorithm for computing mean first passage times of Markov chains.
Applied Mathematics and Computation,
Vol. 250,
Issue. ,
p.
372.
Lin, Hongying
and
Zhou, Bo
2017.
On sharp bounds for spectral radius of nonnegative matrices.
Linear and Multilinear Algebra,
Vol. 65,
Issue. 8,
p.
1554.


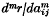 be the
be the 