Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Das, G.
Ghosh, Tulika
and
Ray, B. K.
1995.
Degree of approximation of functions in the Hölder metric by (e, c) means.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 105,
Issue. 3,
p.
315.


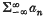 with partial sums {
with partial sums {