Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T18:56:03.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering properties of open continuous mappings having two valences between Riemann surfaces

Published online by Cambridge University Press:  24 October 2008

Abdallah Lyzzaik
Abdallah Lyzzaik
Affiliation:
Department of Mathematics, American University of Beirut, Beirut, Lebanon
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 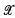be an open Riemann surface with finite genus and finite number of boundary components, and let 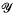be a closed Riemann surface. An open continuous function from 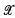to 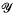is termed a (p, q)-map, 0 < q < p, if it has a finite number of branch points and assumes every point in 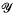either p or q times, counting multiplicity, with possibly a finite number of exceptions. These comprise the most general class of all non-trivial functions having two valences between 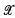and .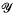

The object of this paper is to study the geometry of (p, q)-maps and establish a generalized embedding theorem which asserts that the image surfaces of (p, q)-maps embed in p-fold closed coverings possibly having branch points off the image surfaces.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 2 , September 1995 , pp. 321 - 340
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ahlfors, L. V. and Sakio, L.. Riemann surfaces (Princeton Univ. Press, 1960).CrossRefGoogle Scholar
[2]Brannan, D. A. and Kirwan, W. E.. Some covering theorems for analytic functions. J. London Math. Soc. (2) 19 (1979), 93–101.CrossRefGoogle Scholar
[3]Brannan, D. A. and Lyzzaik, A. K.. Some covering properties of locally-univalent functions. Ann. Acad. Sei. Fenn. Ser. A I Math. 13 (1988), 3–23.CrossRefGoogle Scholar
[4]Carne, K., Ortel, M. and Smith, W.. Multiplicities of locally one-to-one continuous maps of the plane. Bull. London Math. Soc. 18 (1987), 438–442.CrossRefGoogle Scholar
[5]Lyzzaik, A. K. and Stephenson, K.. The structure of open continuous mappings having two valences. Trans. Amer. Math. Soc. 327 (1991), 525–566.CrossRefGoogle Scholar
[6]Lyzzaik, A. K. and Styer, D.. A covering surface conjecture of Brannan and Kirwan. Bull. London Math. Soc. 14 (1982), 39–42.CrossRefGoogle Scholar
[7]Massey, W. S.. Algebraic topology: An introduction (Springer-Verlag, 1977).Google Scholar
[8]Ortel, M. and Smith, W.. A covering theorem for continuous locally univalent maps of the plane. Bull. London Math. Soc. 18 (1986), 359–363.CrossRefGoogle Scholar
[9]Srebro, U.. Deficiences of immersions. Pacific J. Math. 113 (1984), 493–496.CrossRefGoogle Scholar
[10]Srebro, U.. Covering theorems for meromorphic functions, J. Analyse Math. 44 (1984/1985), 235–250.CrossRefGoogle Scholar
[11]Srebro, U. and Wajnryb, B.. Covering theorems for Riemann surfaces. J. Analyse Math. 46 (1986), 283–303.CrossRefGoogle Scholar
[12]Srebro, U.. Covering theorems for open surfaces. Proceedings of the 1985 Georgia Topology Conference: Geometry and Topology (Dekker, 1987), pp. 265–275.Google Scholar
[13]Stoïlow, S.. Principes topologiques de la théorie des fonctions analytiques (Gauthier-Villars, 1938).Google Scholar