Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T13:19:00.102Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence rates in the law of large numbers. II†

Published online by Cambridge University Press:  24 October 2008

V. K. Rohatgi
V. K. Rohatgi
Affiliation:
Catholic University of America, Washington, D.C., U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let {Xn: n ≥ 1} be a sequence of independent random variables and write 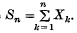Suppose that the random vairables Xn are uniformly bounded by a random variable X in the sense that

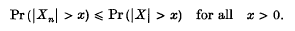
Set qn(x) = Pr(|Xn| > x) and q(x) = Pr(|Xn| > x). If qn ≤ q and E|X|r < ∞ with 0 < r < 2 then we have (see Loève(4), 242)

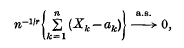
where ak = 0, if 0 < r < 1, and = EXk if 1 ≤ r < 2 and ‘a.s.’ stands for almost sure convergence. the purpose of this paper is to study the rates of convergence of

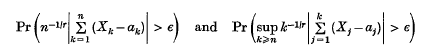
to zero for arbitrary ε > 0. We shall extend to the present context, results of (3) where the case of identically distributed random variables was treated. The techniques used here are strongly related to those of (3).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 2 , April 1968 , pp. 485 - 488
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baum, L. E. and Katz, M.Convergence rates in the law of large numbers. Trans. Amer. Math. Soc. 120 (1965), 108–123.CrossRefGoogle Scholar
(2)Baum, L. E., Katz, M. and Read, R. R.Exponential convergence rates for the law of large numbers. Trans. Amer. Math. Soc. 102 (1962), 187–199.CrossRefGoogle Scholar
(3)Heyde, C. C. and Rohatgi, V. K.A pair of complementary theorems on convergence rates in the law of large numbers. Proc. Cambridge Philos. Soc. 63 (1967), 73–82.CrossRefGoogle Scholar
(4)Lo`ve, M.Probability theory, 3rd edition. Van Nostrand, New York (1963).Google Scholar