Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T13:13:28.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing locales from quantales

Published online by Cambridge University Press:  24 October 2008

Susan B. Niefield  and
Kimmo I. Rosenthal
Susan B. Niefield
Affiliation:
Department of Mathematics, Union College, Schenectady, New York 12308
Kimmo I. Rosenthal
Affiliation:
Department of Mathematics, Union College, Schenectady, New York 12308
Get access Rights & Permissions [Opens in a new window]

Extract

We recall that a locale is a complete lattice L satisfying a ∧ (∨bα) = ∨(a ∧ bα), for all a ∈ L, and {bα} ⊆ L. Examples of locales include the lattices 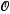(X) of open subsets of topological spaces X. Following Joyal and Tierney [7], a morphism f: L → M of locales is a ∨-, ∧-, and τ-preserving map. Such functions are sometimes called ‘frame homomorphisms’, in which case the right adjoint f*:M → L (which exists since f preserves ∨) is then called a ‘morphism of locales’.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 2 , September 1988 , pp. 215 - 234
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Banaschewski, B. and Harting, R.. Lattice aspects of radical ideals and choice principles. Proc. London Math. Soc. (3) 50 (1985), 385–404.CrossRefGoogle Scholar
[2]Borceux, F. and van den Bossche, G.. Algebra in a Localic Topos with Applications to Ring Theory. Lecture Notes in Math. vol. 1038 (Springer-Verlag, 1983).CrossRefGoogle Scholar
[3]Borceux, F. and van den Bossche, G.. Quantales and their sheaves. Order 3 (1986), 61–87.CrossRefGoogle Scholar
[4]Dixmier, J.. C*-Algebras (North Holland, 1977).Google Scholar
[5]Dowker, C. H. and Strauss, D.. Quotient frames and subspaces. Proc. London Math. Soc. (3) 16 (1966), 275–96.CrossRefGoogle Scholar
[6]Johnstone, P. T.. Stone Spaces. Cambridge Studies in Advanced Math. no. 3 (Cambridge University Press, 1982).Google Scholar
[7]Joyal, A. and Tierney, M.. An Extension of the Galois Theory of Grothendieck. Mem. Amer. Math. Soc. no. 309 (American Mathematical Society, 1984).CrossRefGoogle Scholar
[8]Kirby, D.. Closure operations on ideals and submodules. J. London Math. Soc. 44 (1969), 283–291.CrossRefGoogle Scholar
[9]Mulvey, C. J.. &. Rend. Circ. Mat. Palermo (2) 12 (1986), 99–104.Google Scholar
[10]Nawaz, M.. Quantales: Quantal Sets. Ph.D. thesis, University of Sussex (1985).Google Scholar
[11]Niefield, S. B. and Rosenthal, K. I.. Spatial sublocales and essential primes. Topology Appl. 26 (1987), 263–269.CrossRefGoogle Scholar
[12]Niefield, S. B. and Rosenthal, K. I.. Lattice theoretic aspects of sheaves of ideals. (In preparation.)Google Scholar
[13]Niefield, S. B. and Rosenthal, K. I.. Componental nuclei. In Proceedings of Category Theory Meeting, Louvain-la-Neuve 1987, Lecture Notes in Math. (Springer-Verlag), to appear.Google Scholar
[14]Simmons, H.. A framework for topology. In Logic Colloquium 77, Studies in Logic and the Foundations of Math. no. 96. (North Holland, 1978), pp. 239–251.CrossRefGoogle Scholar
[15]Simmons, H.. Two-sided multiplicative lattices and ring radicals. (Preprint).Google Scholar