No CrossRef data available.
Compactifications and A-compactifications of frames. Proximal frames
Published online by Cambridge University Press: 24 October 2008
Extract
The aim of this paper is to give two new descriptions of the ordered set 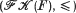 of all (up to equivalence) regular compactifications of a completely regular frame. F and to introduce and study the notion of A-frame as a generalization of the notion of Alexandroff space (known also as zero-set space) (Alexandroff[l], Gordon[15]). A description of the ordered set of all (up to equivalence) A-compactifications of an A-frame by means of an ordered by inclusion set of some distributive lattices (called AP-sublattices) is obtained. It implies that any A-frame has a greatest A-compactification and leads to the descriptions of
of all (up to equivalence) regular compactifications of a completely regular frame. F and to introduce and study the notion of A-frame as a generalization of the notion of Alexandroff space (known also as zero-set space) (Alexandroff[l], Gordon[15]). A description of the ordered set of all (up to equivalence) A-compactifications of an A-frame by means of an ordered by inclusion set of some distributive lattices (called AP-sublattices) is obtained. It implies that any A-frame has a greatest A-compactification and leads to the descriptions of 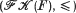 A new category
A new category 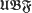 isomorphic to the category
isomorphic to the category 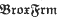 of proximal frames is introduced. A question for compactifications of frames analogous to the R. Chandler's question [8, p. 71] for compactifications of spaces is formulated and solved. Many results of [1], [3], [15], [23], [9], [10] and [11] are generalized.
of proximal frames is introduced. A question for compactifications of frames analogous to the R. Chandler's question [8, p. 71] for compactifications of spaces is formulated and solved. Many results of [1], [3], [15], [23], [9], [10] and [11] are generalized.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 2 , February 1996 , pp. 321 - 339
- Copyright
- Copyright © Cambridge Philosophical Society 1996


