Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T02:18:51.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact groups with a set of positive Haar measure satisfying a nilpotent law

Part of: Abstract harmonic analysis Compact groups Probabilistic methods in group theory

Published online by Cambridge University Press:  19 July 2021

ALIREZA ABDOLLAHI  and
MEISAM SOLEIMANI MALEKAN
ALIREZA ABDOLLAHI
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Statistics, University of Isfahan, Isfahan81746-73441, Iran. e-mails: [email protected], [email protected]
MEISAM SOLEIMANI MALEKAN
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Statistics, University of Isfahan, Isfahan81746-73441, Iran. e-mails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The following question is proposed by Martino, Tointon, Valiunas and Ventura in [4, question 1·20]:

Let G be a compact group, and suppose that

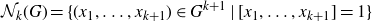\[\mathcal{N}_k(G) = \{(x_1,\dots,x_{k+1}) \in G^{k+1} \;|\; [x_1,\dots, x_{k+1}] = 1\}\]
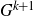has positive Haar measure in $G^{k+1}$ . Does G have an open k-step nilpotent subgroup?

We give a positive answer for 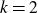$k = 2$ .

MSC classification

Primary: 22C05: Compact groups 43A05: Measures on groups and semigroups, etc.
Secondary: 20P05: Probabilistic methods in group theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 2 , September 2022 , pp. 329 - 332
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Folland, G. B.. A Course in Abstract Harmonic Analysis. Stud. Adv. Math. (Taylor & Francis, London, 1994).Google Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis: Structure and Analysis for Compact Groups Analysis on Locally Compact Abelian Groups. Grundlehren Math. Wiss. (Springer, Berlin, 2013).Google Scholar
Hofmann, K. H. and Russo, F. G.. The probability that x and y commute in a compact group. Math. Proc. Camb. Phils. Soc. 153 no. 3, (2012), 557–571.10.1017/S0305004112000308CrossRefGoogle Scholar
Martino, A., Tointon, M. C. H., Valiunas, M. and Ventura, E.. Probabilistic nilpotence in infinite groups. to appear in Israel J. Math. Google Scholar
Soleimani Malekan, M., Abdollahi, A. and Ebrahimi, M.. Compact groups with many elements of bounded order. J. Group Theory 23, no. 6 (2020), 991–998.Google Scholar