The Cauchy property of the generalised Perron intergrals
Published online by Cambridge University Press: 24 October 2008
Extract
1. Saks calls an integral complete if it satisfies two conditions, of which one, the condition (C), is as follows.
If f(x) is defined in (a, b) and is integrable in each interval (a + ε, b − η), where a < a + ε < b − η < b, and
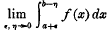
exists, then f(x) is integrable in (a, b) and the integral over (a, b) is equal to the above limit.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 1 , January 1934 , pp. 15 - 18
- Copyright
- Copyright © Cambridge Philosophical Society 1934
References
* Saks, S., Fundamenta Math. 15 (1930), 242–262 (251).CrossRefGoogle Scholar
† Alexandroff, P., Math. Zeitschrift, 20 (1924), 213–222.CrossRefGoogle Scholar
‡ Burkill, J. C., Math. Zeitschrift, 34 (1931), 270–278CrossRefGoogle Scholar; Proc. London Math. Soc. (2), 34 (1932), 314–322.Google Scholar
* Compare Burkill, J. C., Math. Zeitschrift 34 (1931), 277.Google Scholar
- 4
- Cited by


