Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T01:09:17.581Z Has data issue: false hasContentIssue false
  • English
  • Français

Borel and projective sets from the point of view of compact sets

Published online by Cambridge University Press:  24 October 2008

Kenneth Kunen  and
Arnold W. Miller
Kenneth Kunen
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Wisconsin 53706
Arnold W. Miller
Affiliation:
Department of Mathematics, The University of Texas, Austin, Texas 78712
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we prove several results concerning the complexity of a set relative to compact sets. We prove that for any Polish space X and Borel set B ⊆ X, if B is not 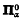, then there exists a compact zero-dimensional P ⊆ X such that p ∩ X is not 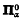. We also show that it is consistent with ZFC that, for any A ⊆ ωω, if for all compact K ⊆ ωωA ∩ K is 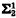, then A is 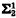. This generalizes to in place of 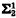assuming the consistency of some hypotheses involving determinacy. We give an alternative proof of the following theorem of Saint-Raymond. Suppose X and Y are compact metric spaces and f is a continuous surjection of X onto Y. Then, for any A ⊆ Y, A is 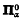in Y iff f−1(A) is 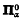in X. The non-trivial part of this result is to show that taking pre-images cannot reduce the Borel complexity of a set. The techniques we use are the definability of forcing and Wadge games.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 3 , November 1983 , pp. 399 - 409
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Becher, H., Partially playful universes. In Cabal Seminar 76–77, Lecture Notes in Math. vol. 689 (Springer-Verlag, 1978).Google Scholar
[2] Bockstein, M.. Un théorème de séparabilité pour les produits topologiques. Fund. Math. 35 (1948), 242–246.CrossRefGoogle Scholar
[3] Heceler, S. H.. On the existence of certain cofinal subsets of ωω. In Proc. of Symp. in Pure Math., vol. 13, part 2, AMS (1974), 155–173.CrossRefGoogle Scholar
[4] Jayne, J. E. and Rogers, C. A.. K-analytic sets. In Analytic Sets (Academic Press, 1980), pp. 1–175.Google Scholar
[5] Jayne, J. E. and Rogers, C. A.. The invariance of the absolute Borel classes. Convex Analysis and Optimization, Research Notes in Math. no. 57 (Pitman, 1982), 119–151.Google Scholar
[6] Jech, T.. Set Theory (Academic Press, 1978).Google Scholar
[7] Kuratowski, K.. Topology, vol. 1 (Academic Press, 1966).Google Scholar
[8] Louveau, A.. A separation theorem for ; sets. Trans. Amer. Math. Soc. 260 (1980), 363–378.Google Scholar
[9] Martin, D. A. and Solovay, R. M.. Internal Cohen extensions. Ann. Math. Logic 2 (1970), 143–178.CrossRefGoogle Scholar
[10] Mathias, A. R. D., Ostaszewski, A. J. and Talagrand, M.. On the existence of an analytic set meeting each compact set in a Borel set. Math. Proc. Cambridge Philos. Soc. 84 (1978), 5–10.CrossRefGoogle Scholar
[11] Miller, A., Some properties of measure and category. Trans. Amer. Math. Soc. 266 (1981), 93–114.CrossRefGoogle Scholar
Miller, A., Corrections. Trans. Amer. Math. Soc. 271 (1982), 347–348.Google Scholar
[12] Rogers, C. A. et al. Analytic Sets (Academic Press, 1980).Google Scholar
[13] Rudin, M. E.. Martin's axiom. In Handbook of Mathematical Logic (North Holland, 1977), pp. 491–501.CrossRefGoogle Scholar
[14] Saint-Raymond, J.. Fonctions Boréliennes sur un quotient. Bull. Soc. Math. 2° série, 100 (1976), 141–147.Google Scholar
[15] Van Wesep, R.. Wadge degrees and descriptive set theory. In Cabal Seminar 76–77, Lecture Notes in Math. vol. 689 (Springer-Verlag, 1978).Google Scholar
[16] Willard, S.. General Topology (Addison-Wesley, 1970).Google Scholar