No CrossRef data available.
Attaching cells to finite complexes, with an application to elliptic spaces
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose that f; Sn → E is a continuous map from the n-sphere to a 1-connected CW complex E, with n ≥ 2. One may suppose that f is a cofibration, so that there is a cofibration sequence 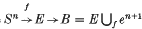 , with f the attaching map of the cell en+1. Consider the homotopy fibre F of the inclusion E ↪ B, so that there is a homotopy fibration
, with f the attaching map of the cell en+1. Consider the homotopy fibre F of the inclusion E ↪ B, so that there is a homotopy fibration 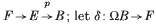 let δ; ΩB → F be the connectant of this fibration. The following definition is given by Félix and Lemaire in [11]:
Definition 1·1. Suppose that k is a field of characteristic p ≥ 0. The attaching map f:Sn → E is:
1. p-inert if
let δ; ΩB → F be the connectant of this fibration. The following definition is given by Félix and Lemaire in [11]:
Definition 1·1. Suppose that k is a field of characteristic p ≥ 0. The attaching map f:Sn → E is:
1. p-inert if 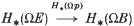 is surjective;
2. p-lazy if
is surjective;
2. p-lazy if 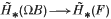 is zero;
where H˜ denotes reduced homology and coefficients are taken in the field k.
is zero;
where H˜ denotes reduced homology and coefficients are taken in the field k.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 3 , April 1996 , pp. 483 - 491
- Copyright
- Copyright © Cambridge Philosophical Society 1996


