Article contents
Asymptotic prime divisors over complete intersection rings
Published online by Cambridge University Press: 02 February 2016
Abstract
Let A be a local complete intersection ring. Let M, N be two finitely generated A-modules and I an ideal of A. We prove that
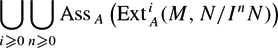 $$\bigcup_{i\geqslant 0}\bigcup_{n \geqslant 0}{\rm Ass}_A\left({\rm Ext}_A^i(M,N/I^n N)\right)$$
$$\bigcup_{i\geqslant 0}\bigcup_{n \geqslant 0}{\rm Ass}_A\left({\rm Ext}_A^i(M,N/I^n N)\right)$$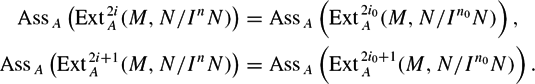 $$\begin{linenomath}\begin{subeqnarray*}
{\rm Ass}_A\left({\rm Ext}_A^{2i}(M,N/I^nN)\right) &=& {\rm Ass}_A\left({\rm Ext}_A^{2 i_0}(M,N/I^{n_0}N)\right), \\
{\rm Ass}_A\left({\rm Ext}_A^{2i+1}(M,N/I^nN)\right) &=& {\rm Ass}_A\left({\rm Ext}_A^{2 i_0 + 1}(M,N/I^{n_0}N)\right).
\end{subeqnarray*}\end{linenomath}$$
$$\begin{linenomath}\begin{subeqnarray*}
{\rm Ass}_A\left({\rm Ext}_A^{2i}(M,N/I^nN)\right) &=& {\rm Ass}_A\left({\rm Ext}_A^{2 i_0}(M,N/I^{n_0}N)\right), \\
{\rm Ass}_A\left({\rm Ext}_A^{2i+1}(M,N/I^nN)\right) &=& {\rm Ass}_A\left({\rm Ext}_A^{2 i_0 + 1}(M,N/I^{n_0}N)\right).
\end{subeqnarray*}\end{linenomath}$$
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 3 , May 2016 , pp. 423 - 436
- Copyright
- Copyright © Cambridge Philosophical Society 2016
References
REFERENCES
A correction has been issued for this article:
- 3
- Cited by
Linked content
Please note a has been issued for this article.


