Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T04:52:10.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximating maps and exact C*-algebras

Published online by Cambridge University Press:  24 October 2008

R. J. Archbold
R. J. Archbold
Affiliation:
University of Aberdeen
Get access Rights & Permissions [Opens in a new window]

Extract

Let A and E be C*-algebras, let A ⊗ B denote the minimal C*-tensor product, and let 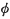ε A *. The right slice map R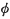: A ⊗ B → B is the unique bounded linear mapping with the property that R 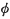(a ⊗ b) = 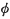(a)b (a ε A, b ε B)(10). A triple (A, B, D), where D is a C*-subalgebra of B, is said to have the slice map property if whenever x ε A ⊗ B and R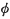(x) 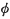D for all 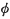ε A* then x ε A ⊗ D). It is known that (A, B, D) has the slice map property whenever A is nuclear (11,13), but it appears to be still unknown whether the nuclearity of B will suffice (unless some extra condition is placed on D (l)).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 91 , Issue 2 , March 1982 , pp. 285 - 289
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Archbold, R. J. and Batty, C. J. K.C*-tensor norms and slice maps. J. London Math. Soc. (2) 22 (1980), 127–138.CrossRefGoogle Scholar
(2)Bunce, J. W.Approximating maps and a Stone-Weierstrass theorem for C*-algebras. Proc. Amer. Math. Soc. 79 (1980), 559–563.Google Scholar
(3)Choi, M. D. and Effros, E. G.Nuclear C*-algebras and the approximation property. Amer. J. Math. 100 (1978), 61–79.CrossRefGoogle Scholar
(4)Effros, E. G. and Lance, E. C.Tensor products of operator algebras. Advances in Math. 25 (1977), 1–34.CrossRefGoogle Scholar
(5)Guichardet, A.Tensor products of C*-algebras. Part 1. Aarhus University Lecture Note Series 12, 1969.Google Scholar
(6)Haagerup, U.An example of a non-nuclear C*-algebra which has the metric approximation property. Invent. Math. 50 (1979), 279–293.CrossRefGoogle Scholar
(7)Kirchberg, E. Positive maps and C*-nuclear algebras. Proc. Int. Conf. on Operator Algebras, Ideals and Their Applications in Theoretical Physics (Leipzig, 1977), (Teubner, Leipzig, 1978), pp. 327–328.Google Scholar
(8)Kirchberg, E. The Fubini theorem for exact C*-algebras. Preprint.Google Scholar
(9)Lance, E. C.Tensor products of non-unital C*-algebras. J. London Math. Soc. (2) 12 (1976), 160–168.CrossRefGoogle Scholar
(10)Tomiyama, J.Applications of Fubini type theorem to the tensor products of C*-algebras. Tohôku Math. J. 19 (1967), 213–226.Google Scholar
(11)Tomiyama, J. Some aspects of the commutation theorem for tensor products of operator algebras. Algèbres d'opérateurs et leurs application en physique mathématique, Colloq. Inter, du C.N.R.S. (no. 274), Marseille, 1977, 417–435.Google Scholar
(12)Wassermann, S.On tensor products of certain group C*-algebras. J. Functional Analysis, 23 (1976), 239–254.CrossRefGoogle Scholar
(13)Wassermann, S.A pathology in the maximal ideal space of L(H) ⊗ L(H). Indiana Univ. Math. J. 27 (1978), 1011–1020.CrossRefGoogle Scholar