Hostname: page-component-6dbcb7884d-wnk8j Total loading time: 0 Render date: 2025-02-14T09:01:35.325Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic sets from the point of view of compact sets

Published online by Cambridge University Press:  24 October 2008

Howard Becker
Howard Becker
Affiliation:
Department of Mathematics and Statistics, University of South Carolina, Columbia, SC 29208, U.S.A., and Department of Mathematics, California Institute of Technology, Pasadena, CA 91125, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

A set A ⊂ ωω is called compactly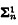 if, for every compact K ⊂ ωω, A ∩ K is 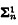. Consider the proposition that every compactly 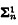set is 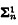. (AD implies that it is true, ZFC + CH implies that it is false.) We are concerned here with whether this is consistent with ZFC, particularly when n = 1. In the case of 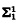sets (that is, analytic sets), this consistency question is due to Fremlin (see [7], page 483, problem 18). Kunen and Miller [3] have proved the following two theorems.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 1 , January 1986 , pp. 1 - 4
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hechler, S. H.. On the existence of certain cofinal subsets of ωω. Proc. of Symp. in Pure Math., 13 (2) (1974), 155–173.CrossRefGoogle Scholar
[2]Kechris, A. S.. Homogeneous trees and projective scales Cabal Seminar 77–79, Lecture Notes in Math., vol. 839 (Springer-Verlag, 1981), 33–74.CrossRefGoogle Scholar
[3]Kunen, K. and Miller, A. W.. Borel and projective sets from the point of view of compactsets. Math. Proc. Cambridge Philos. Soc. 94 (1983), 399–409.CrossRefGoogle Scholar
[4]Martin, D. A.. Borel and Projective Games, to appear.Google Scholar
[5]Martin, D. A. and Solovay, R. M.. A basis theorem for sets of reals. Ann of Math. 89 (1969), 138–160.CrossRefGoogle Scholar
[6]Moschovakis, Y. N.. Descriptive Set Theory (North-Holland, 1980).Google Scholar
[7]Rogers, C. A. et al. Analytic Sets (Academic Press, 1980).Google Scholar