Analysis of tangential properties of curves of infinite length
Published online by Cambridge University Press: 24 October 2008
Extract
In a recent paper (1) I have studied tangential properties of sets of infinite measure. This note represents a complementary study of sets and, in particular of arcs, of σ-finite linear measure. Suppose we have a linearly measurable set E of infinite measure that can be represented as the sum 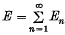 of sets of finite measure. Write En = En, 1 + En, 2, where En, 1 is the set of regular points of En and En, 2 that of irregular ones. The set F = ΣEn, 1 is a regular component of E and the set G = ΣEn, 2 an irregular one. A tangent toEn exists at almost all points of En, 1 and at almost no points of En, 2. Denote by Tn the set of all tangents to En and by T the sum-set ΣTn. T will be called a tangent-set to E. Lines of T are defined corresponding to almost all points of F and to the points of a subset of G of measure zero.
of sets of finite measure. Write En = En, 1 + En, 2, where En, 1 is the set of regular points of En and En, 2 that of irregular ones. The set F = ΣEn, 1 is a regular component of E and the set G = ΣEn, 2 an irregular one. A tangent toEn exists at almost all points of En, 1 and at almost no points of En, 2. Denote by Tn the set of all tangents to En and by T the sum-set ΣTn. T will be called a tangent-set to E. Lines of T are defined corresponding to almost all points of F and to the points of a subset of G of measure zero.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 1 , January 1957 , pp. 69 - 72
- Copyright
- Copyright © Cambridge Philosophical Society 1957
References
REFERENCES
- 1
- Cited by


