Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dikshit, H. P.
1972.
Total and absolute total-effective product method.
Annali di Matematica Pura ed Applicata,
Vol. 94,
Issue. 1,
p.
11.
Dikshit, H. P.
and
Kumar, A.
1975.
Absolute total-effectiveness of (N, pn) means. I.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 77,
Issue. 1,
p.
103.
Kumar, Arun
1982.
Absolute total-effectiveness of a total effective (𝑁,𝑝_{𝑛}) method.
Proceedings of the American Mathematical Society,
Vol. 84,
Issue. 4,
p.
497.
Rhoades, B. E.
1986.
Matrix summability of Fourier series based on inclusion theorems.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 3,
p.
545.
Kuttner, B.
and
Rhoades, B. E.
1989.
Absolute Nörlund matrix summability of Fourier series based on inclusion theorems.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 105,
Issue. 2,
p.
319.


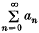 be a given infinite series with the sequence of its partial sums {
be a given infinite series with the sequence of its partial sums {