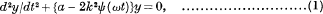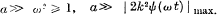Other
The Mathematical Association
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 45-46
-
- Article
- Export citation
Joint Report of the Council and Executive Committee, 1944
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 46-48
-
- Article
- Export citation
The Annual General Meeting: 1946
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 48
-
- Article
- Export citation
Gleanings Far and Near
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 48
-
- Article
- Export citation
Teachers and Examiners
Presidential Address to the Mathematical Association, April, 1945
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 49-56
-
- Article
- Export citation
Other
New South Wales Branch
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 56
-
- Article
- Export citation
Research Article
The Mathematical Theory of the Influence of Thin Films on the Reflection and Transmission of Light
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 57-65
-
- Article
- Export citation
On the Three-Cusped Hypocycloid
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 66-67
-
- Article
- Export citation
Hill's Differential Equation
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 68-69
-
- Article
- Export citation
Mathematical Notes
1813. Pythagoras’ theorem
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 70
-
- Article
- Export citation
1814. The complete quadrilateral
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 70-71
-
- Article
- Export citation
1815. The pedal lines of a given point
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 71
-
- Article
- Export citation
1816. Mental multiplication
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 71-72
-
- Article
- Export citation
1817. On Note 1730 (Gazatte, XXVIII, July, 1944)
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 72
-
- Article
- Export citation
1818. On Note 1717 (“ Inaccessible heights and distances ”)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 72-74
-
- Article
- Export citation
1819. Some properties of plane cubic curves
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 74-75
-
- Article
- Export citation
1820. A note on a cubic and an associated family of conics
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 75-77
-
- Article
- Export citation
1821. On “bending momentum round corners”
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 77-79
-
- Article
- Export citation
1822. A point in teaching dynamics
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 79-80
-
- Article
- Export citation
1823. Curiosités arithmétiques
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 80
-
- Article
- Export citation