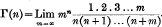Research Article
On the Connection between the Inscribed and Escribed Circles of a Triangle
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 177-180
-
- Article
- Export citation
Notes on Elementary Dynamics V
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 180-184
-
- Article
- Export citation
Mathematical Notes
54. Note on Section VI. of Professor Tanner's article on " A Class of Algebraic Functions" (p. 153)
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 184
-
- Article
- Export citation
55. Euclid IV. 12, 13, 14
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 184-185
-
- Article
- Export citation
56. Note on the Simson Line
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 185-186
-
- Article
- Export citation
57. Criteria of Divisibility
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 186-187
-
- Article
- Export citation
58. On the general proof of the rule for finding the product of two algebraic expressions
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 187-188
-
- Article
- Export citation
59. On the Circular Measure of Angles
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 188-189
-
- Article
- Export citation
60. Note on the formula
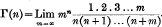
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 189-190
-
- Article
- Export citation
61. A Transformation in Elementary Geometry
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 190
-
- Article
- Export citation
Other
Examination Questions and Problems
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 191-193
-
- Article
- Export citation
Solutions
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 193-200
-
- Article
- Export citation
Books Received
Books, Magazines, etc., Received
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 200
-
- Article
- Export citation
Front Matter
MAG volume 1 issue 14 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. f1-f2
-
- Article
- Export citation
Back Matter
MAG volume 1 issue 14 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. b1-b2
-
- Article
- Export citation