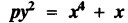Articles
How to choose your relations
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 193-202
-
- Article
- Export citation
Optimising the acceleration due to gravity on a planet's surface
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 203-215
-
- Article
- Export citation
Integrating expressions of the form
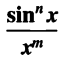 and others
and others
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 216-223
-
- Article
- Export citation
An unexpected use of primes: solving sudokus by calculator
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 224-232
-
- Article
- Export citation
Rugby conversions: a 3-dimensional model
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 233-238
-
- Article
- Export citation
(The Bride's Chair)2
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 239-246
-
- Article
- Export citation
Stop-sign theorems and binomial coefficients*
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 247-261
-
- Article
- Export citation
A footnote to the theory of double integrals
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 262-269
-
- Article
- Export citation
Regarding a generalisation of Ioachimescu's constant
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 270-283
-
- Article
- Export citation
Notes 94.11 to 94.25
94.11 Visualising continued fractions
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 284-290
-
- Article
- Export citation
94.12 The non-existence of integer solutions to
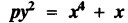
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 290-294
-
- Article
- Export citation
94.13 Group theory lends a hand to number theory
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 294-296
-
- Article
- Export citation
94.14 On an identity involving binomial coefficients via arctan(x)
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 296-298
-
- Article
- Export citation
94.15 Napier's table of logarithms
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 299-303
-
- Article
- Export citation
94.16 Irrational roots revisited
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 303-304
-
- Article
- Export citation
94.17 Evaluating the Euler constant
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 304-306
-
- Article
- Export citation
94.18 Proof without words: Two inequalities proved by convexity
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 306-308
-
- Article
- Export citation
94.19 A calculus-based approach to the von Staudt-Clausen theorem
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 308-312
-
- Article
- Export citation
94.20 An interesting constraint on cutting corners
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 312-314
-
- Article
- Export citation
94.21 Grandma, grandaunts and distant cousins
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 314-316
-
- Article
- Export citation

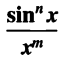 and others
and others
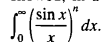 One can show in a simpler manner, however, how to evaluate, for integers
One can show in a simpler manner, however, how to evaluate, for integers 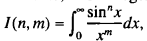 where
where 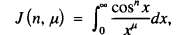 where such an integral converges.
where such an integral converges.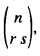 where
where 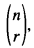 , and then use this expanded notation to develop theorems involving 8 binomial coefficients, analogous to the Star of David Theorem, which. in its original form, involved the 6 neighbours of a given binomial coefficient in the Pascal Triangle (see Section 3), that appeared in [1,2,3,4,5,6,7,8,9].
, and then use this expanded notation to develop theorems involving 8 binomial coefficients, analogous to the Star of David Theorem, which. in its original form, involved the 6 neighbours of a given binomial coefficient in the Pascal Triangle (see Section 3), that appeared in [1,2,3,4,5,6,7,8,9].
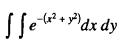
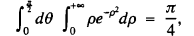
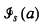 of the sequence
of the sequence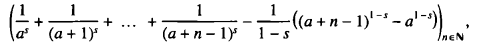
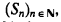 , defined by
, defined by 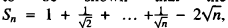 , for each
, for each 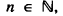 , is convergent and its limit lies between -2 and -1.
, is convergent and its limit lies between -2 and -1.