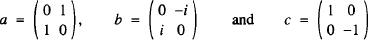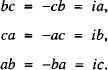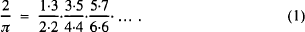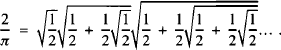Articles
Progressing through mathematics
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 385-400
-
- Article
- Export citation
The perfect cipher
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 401-411
-
- Article
- Export citation
Codes, not ciphers
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 412-425
-
- Article
- Export citation
Forming groups with 4 × 4 matrices
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 426-429
-
- Article
- Export citation
The tables of John Wallis and the discovery of his product π
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 430-437
-
- Article
- Export citation
Eigencircles and associated surfaces
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 438-449
-
- Article
- Export citation
Mathematical Rugby
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 450-463
-
- Article
- Export citation
Notes 94.26 to 94.40
94.26 Computing quadratic fundamental units
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 464-467
-
- Article
- Export citation
94.27 To your hearts' content
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 467-473
-
- Article
- Export citation
94.28 The hyperexponential function
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 473-476
-
- Article
- Export citation
94.29 On two properties of the inverse Hilbert matrix
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 476-479
-
- Article
- Export citation
94.30 Ratios of volumes related to the odd extension of a power function
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 479-486
-
- Article
- Export citation
94.31 Approximations for π and e
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 486-488
-
- Article
- Export citation
94.32 The recursive nature of Euler's formula for harmonic series
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 488-492
-
- Article
- Export citation
94.33 Short proofs of Jensen's and Levinson's Inequalities
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 492-495
-
- Article
- Export citation
94.34 Regular polygons with integer coordinates
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 495-498
-
- Article
- Export citation
94.35 Popularising the ASS pseudo-congruence theorem
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 499-502
-
- Article
- Export citation
94.36 Wheels within wheels
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 502-505
-
- Article
- Export citation
94.37 Multinomial distributions and knockout tournaments
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 505-509
-
- Article
- Export citation
94.38 The truth table of the logical implication
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 509-513
-
- Article
- Export citation