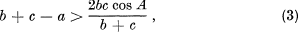Research Article
The Scientific Exploration of Outer Space Since the Time of Galileo: I. Observational Astronomy and Astrophysics*
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 183-198
-
- Article
- Export citation
An Early Best Seller: Francis Walkingame’s ‘The Tutor’s Assistant’
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 199-208
-
- Article
- Export citation
Rotation Groups and Permutation Groups
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 209-210
-
- Article
- Export citation
The Axioms of Non-Metrical Geometry
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 210-214
-
- Article
- Export citation
The Laplace Transform
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 215-219
-
- Article
- Export citation
On a Problem in Graph Theory
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 220-223
-
- Article
- Export citation
Other
The Mathematical Association
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 223
-
- Article
- Export citation
Research Article
Two Inequalites for a Triangle
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 224-225
-
- Article
- Export citation
The Summer Research Institute of the Canadian Mathematical Congress
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 225-228
-
- Article
- Export citation
Priorities in the Reform of Mathematics Teaching
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 228-232
-
- Article
- Export citation
Other
A New Permanent Cross Calendar
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 233
-
- Article
- Export citation
Mathematical Notes
3065. Division by 7
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 234-235
-
- Article
- Export citation
3066. A set of square matrices
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 235-236
-
- Article
- Export citation
3067. Triangular numbers
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 236-237
-
- Article
- Export citation
3068. A simple proof of a result on diophantine approximation
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 237-238
-
- Article
- Export citation
3069. An application of Euclid's algorithm
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 238-239
-
- Article
- Export citation
3070. Why comparisons (in arithmetic) are odious
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 239-240
-
- Article
- Export citation
3071. Canting a rifle
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 240-242
-
- Article
- Export citation
3072. Kinetic energy and relative velocity
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 242-243
-
- Article
- Export citation
3073. Alternative proof for formula in Note 1365
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 243-244
-
- Article
- Export citation