No CrossRef data available.
Article contents
When does 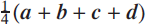 $${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$ give the centre of mass of a quadrilateral?
$${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$ give the centre of mass of a quadrilateral?
Published online by Cambridge University Press: 16 February 2023
Extract
Having done the formula
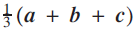 $${\textstyle{1 \over 3}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c})$$
for the centre of mass of a uniform triangular lamina with vertices at position vectors a, b, c, I was recently asked in class whether
$${\textstyle{1 \over 3}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c})$$
for the centre of mass of a uniform triangular lamina with vertices at position vectors a, b, c, I was recently asked in class whether
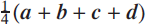 $${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$
was the corresponding result for a uniform quadrilateral lamina. It is easy to give examples where the formula does work (squares, rectangles, parallelograms), but equally clear from examples such as the trapezium in Figure 1, where the centre of mass is located below the centre line on which
$${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$
was the corresponding result for a uniform quadrilateral lamina. It is easy to give examples where the formula does work (squares, rectangles, parallelograms), but equally clear from examples such as the trapezium in Figure 1, where the centre of mass is located below the centre line on which
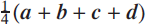 $${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$
lies, that it does not always work.
$${\textstyle{1 \over 4}}(\boldsymbol {a} + \boldsymbol {b} + \boldsymbol {c} + \boldsymbol {d})$$
lies, that it does not always work.
- Type
- Teaching Notes
- Information
- Copyright
- © The Authors, 2023. Published by Cambridge University Press on behalf of The Mathematical Association



