The trisectrix and Langley's problem

Extract

If a circle rolls without slipping around an equal fixed circle, then a point carried by the rolling circle traces out a limaçon of Pascal. (This is Etienne Pascal, father of Blaise. The word limaçon is derived from the Latin limax, a snail.) If the fixed and rolling circles have radius 1, and the point P carried by the rolling wheel is distant a from its centre, then for a > 1 the limaçon has an inner and an outer loop, joining up at a node. For a = 1 it has a cusp, and is then a cardioid, so-called because it is heart-shaped. See Figure 1, where we have plotted the cases a = 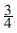$${3 \over 4}$$ , a = 1 and a = 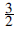$${3 \over 2}$$ .