No CrossRef data available.
Article contents
The Transformation y=f’(x)
Published online by Cambridge University Press: 03 November 2016
Extract
The transformation y=f'(x) on the roots of
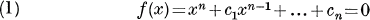
is intersting to study on account of the fact that it leads to a transformed equation whose constant term is, the discriminant of f(x)=0. It is easy to see that this property holds, for, writing f(x) in the factored form
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1933
References
page 251 note * In the American Mathematical Monthly, vol. 38 (1931), 185-6, I have used the transformation y = x2 to obtain the cubic discriminant, but in a different and less convenient way.
page 252 note * See School Science and Mathematics, vol. 29 (1929), 474-76, for a treatment based on essentially this transformation.
page 252 note † For details the reader may consult Dickson, First Course in the Theory of Equations, 1922, section 60.
page 254 note * See Dickson, Modem Algebraic Theories, 1926, 245; Kiepert, Journal für die reine und angewandte Mathematik, vol. 87 (1879), 132.
page 255 note * See, for example, Brioschi, Math. Annalen, vol. 13 (1878), 143-53.
page 255 note † yi (i = 1,2, ... 5) are the roots of the transformed equation.


