So-Called Cases of Failure in the Solution of Linear Differential Equations

Extract

There are two ways in which the solution of a particular linear differential equation may “fail” although the solulion of a more general equation obtained by replacing certain constants by parameters is complete.

where D as usual stands for d/dx.

For the general equation

(D — l)(D — m)y = e^nx

the perfectly general solution is

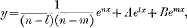
A, B being independent arbitrary constants, but if we attempt to apply this solution to the particular equation (l), we find in the first place that the coincidence of n with l and m renders the first term infinite, and in the second place that the coincidence of m with l leaves us with only one effective constant, A + B. The method by which in the commoner textbooks the passage from the general solution to that of a particular equation is made in such cases as this is unconvincing.