Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T16:22:52.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Sequences of averages

Published online by Cambridge University Press:  01 August 2016

Jim Gowers ,
Graham Davis  and
Elizabeth Miles
Jim Gowers
Affiliation:
Department of Computer Studies and Mathematics, Bristol Polytechnic, Bristol BS16 1QY
Graham Davis
Affiliation:
Department of Computer Studies and Mathematics, Bristol Polytechnic, Bristol BS16 1QY
Elizabeth Miles
Affiliation:
Department of Computer Studies and Mathematics, Bristol Polytechnic, Bristol BS16 1QY
Get access Rights & Permissions [Opens in a new window]

Extract

A very simple way of generating a sequence is to take two starting values, a1 and a2, and construct a3 as their arithmetic mean, a4 as the mean of a2 and a3 and so on. This sequence always converges to the limit 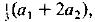and seems to be fairly widely known as a topic for investigation in schools and colleges. It can immediately be generalised to the case of k starting values, and this forms a good subject for investigation using a micro-computer. It seems likely that such a simple set-up has arisen independently many times. One emergence occurred about ten years ago at a conference of the Association of Teachers of Mathematics, where the originator introduced it under the fictitious name ‘Littov sequences’. It has recently resurfaced at a Department of Education and Science conference.

Type
Research Article
Information
The Mathematical Gazette , Volume 70 , Issue 453 , October 1986 , pp. 200 - 203
Copyright
Copyright © The Mathematical Association 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Vertannes, M.G., Littov’s mean value theorem, Math. Educ.for Teaching, 4, 28–30 (1984).Google Scholar
2. Hale, D.S. and Taylor, R.S., A computer-aided investigation, Maths in Schools, 14, 36–37 (1985).Google Scholar
3. Cox, D.R. and Miller, H.D., The theory of stochastic processes. Methuen (1965).Google Scholar
4. Durran, J.H., Statistics and probability. Cambridge University Press (1970).Google Scholar