No CrossRef data available.
Article contents
The Roots of Certain Determinantal Equations
Published online by Cambridge University Press: 03 November 2016
Extract
In her paper (Gazette, May 1950, p. 94) on the roots of two types of determinantal equation, M. J. Moore obtained various results by elementary but somewhat complicated methods . In this note, these results are obtained by a simpler method, which moreover helps to exhibit their real significance. The essential facts are expressed by the following theorem:
THEOREM I. If a rational function of x has poles and zeros (including a possible pole or zero at infinity) which are all real, simple and strictly alternate, then its partial fraction expansion
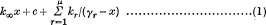
has coefficients kr (including k∞ if non-zero) all of one sign, while its reciprocal has expansion coefficients all of the opposite sign.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mathematical Association 1952
References
(page no 271 note *) This is of order n, with its (r , s) element equal to ![]() ,
,![]() ,
,![]() ,otherwise 0, where
,otherwise 0, where ![]() .
.
(page no 272 note *) This is of order n, with its (r , s) element equal to ![]() otherwise 0, where
otherwise 0, where ![]()


