Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T22:11:41.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting the general cubic: a simplification of Cardano's solution

Published online by Cambridge University Press:  11 October 2023

Hsin-Chieh Liao ,
Mark Saul  and
Peter J.-S Shiue
Hsin-Chieh Liao
Affiliation:
Department of Mathematics, University of Miami, Florida 33146, USA e-mail: [email protected]
Mark Saul
Affiliation:
Nine Nine Cultural and Educational Foundation, 9F, No. 300, Sec 3. Roosevelt Road, Zhongzheng Dist., Taipei City 10900, Taiwan e-mail: [email protected]
Peter J.-S Shiue
Affiliation:
Department of Mathematical Sciences, University of Nevada, Las Vegas NV 89154-4020, USA e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Given a polynomial equation x3 + ax2 + bx + c = 0 of degree 3 with real coefficients, we may translate the variable by replacing x with x − 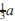to make the quadratic term vanish. We then obtain a simpler equation x3 + px + q = 0 where 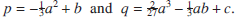Therefore, in order to solve a polynomial equation of degree 3, it is sufficient to solve equations of the form x3 + px + q = 0.

Type
Articles
Information
The Mathematical Gazette , Volume 107 , Issue 570 , November 2023 , pp. 438 - 444
Check for updates
Copyright
© The Authors, 2023 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Harris, J. W., Stocker, H., Handbook of mathematics and computational science, Springer-Verlaine (1998).CrossRefGoogle Scholar
Burton, D. M., Abstract algebra, Wm. C. Brown (1988).Google Scholar
Gilbert, L., Gilbert, J., Elementary modern algebra (8th edn), Cengage Learning (2015).Google Scholar
Sylvester, J. J., On a remarkable discovery in the theory of canonical forms and of hyperdeterminants, Math. Mag. 2 (1851) pp. 391–410.Google Scholar
Chen, W.Y.C., Cubic equations through the looking glass of Sylvester, College Math. J., 53(5) (2022) pp. 396–398.CrossRefGoogle Scholar
Liao, H. C., Shiue, P. J. -S, Cubic equations revisited (in Chinese), Math Media, 46(1) (2022) pp. 33–39.Google Scholar